2026-01-18 Daily Challenge

Posted on:
Posted modified:
In: DailyChallenge

Today I have done leetcode's [January LeetCoding Challenge](https://leetcode.com/problems/Largest Magic Square /) with cpp.

January LeetCoding Challenge 18

Description

Largest Magic Square

A k x k magic square is a k x k grid filled with integers such that every row sum, every column sum, and both diagonal sums are all equal. The integers in the magic square do not have to be distinct. Every 1 x 1 grid is trivially a magic square.

Given an m x n integer grid, return the size (i.e., the side length k) of the largest magic square that can be found within this grid.

 

Example 1:

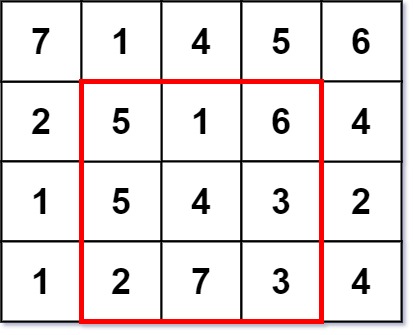
Input: grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
Output: 3
Explanation: The largest magic square has a size of 3.
Every row sum, column sum, and diagonal sum of this magic square is equal to 12.
- Row sums: 5+1+6 = 5+4+3 = 2+7+3 = 12
- Column sums: 5+5+2 = 1+4+7 = 6+3+3 = 12
- Diagonal sums: 5+4+3 = 6+4+2 = 12

Example 2:

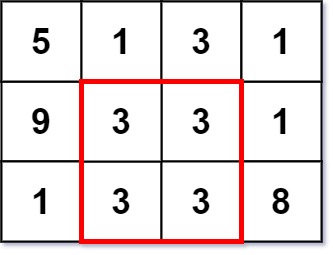
Input: grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]]
Output: 2

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 50
  • 1 <= grid[i][j] <= 106

Solution

class Solution {
  bool ok(const vector<vector<int>>& grid, int startCol, int startRow, int k) {
    int target = accumulate(grid[startRow].begin() + startCol, grid[startRow].begin() + startCol + k, 0);
    // cout << startRow << ' ' << startCol << ' ' << k << ' ' << target << endl;
    for(int i = 0; i < k; ++i) {
      int sum = 0;
      for(int j = 0; j < k; ++j) {
        sum += grid[startRow + i][startCol + j];
      }
      if(sum != target) return false;
      sum = 0;
      for(int j = 0; j < k; ++j) {
        sum += grid[startRow + j][startCol + i];
      }
      if(sum != target) return false;
    }
    int sum = 0;
    for(int i = 0; i < k; ++i) {
      sum += grid[startRow + i][startCol + i];
    }
    if(sum != target) return false;
    sum = 0;
    for(int i = 0; i < k; ++i) {
      sum += grid[startRow + k - 1 - i][startCol + i];
    }
    if(sum != target) return false;
    return true;
  }
public:
  int largestMagicSquare(vector<vector<int>>& grid) {
    int rows = grid.size();
    int cols = grid.front().size();
    for(int k = min(rows, cols); k > 1; --k) {
      for(int row = 0; row + k <= rows; ++row) {
        for(int col = 0; col + k <= cols; ++col) {
          if(ok(grid, col, row, k)) return k;
        }
      }
    }
    return 1;
  }
};

// Accepted
// 80/80 cases passed (34 ms)
// Your runtime beats 49.43 % of cpp submissions
// Your memory usage beats 87.43 % of cpp submissions (12.9 MB)
Algorithm