Today I have done leetcode's March LeetCoding Challenge with cpp.

March LeetCoding Challenge 22

Description

Count the Number of Complete Components

You are given an integer n. There is an undirected graph with n vertices, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting vertices ai and bi.

Return the number of complete connected components of the graph.

A connected component is a subgraph of a graph in which there exists a path between any two vertices, and no vertex of the subgraph shares an edge with a vertex outside of the subgraph.

A connected component is said to be complete if there exists an edge between every pair of its vertices.

Example 1:

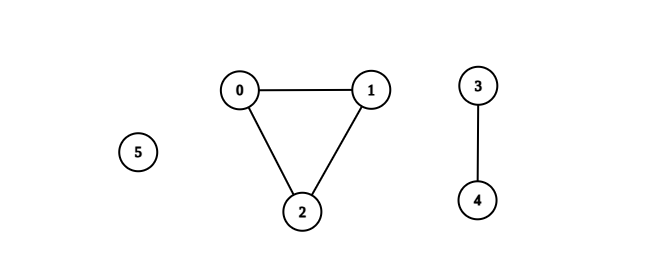
Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
Output: 3
Explanation: From the picture above, one can see that all of the components of this graph are complete.

Example 2:

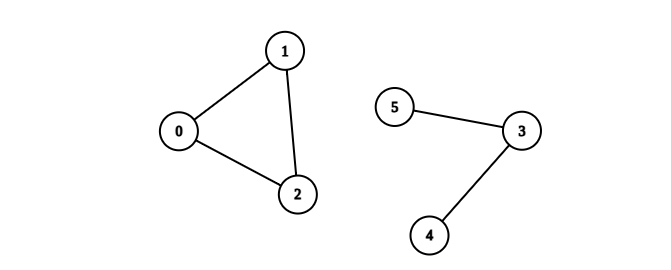
Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
Output: 1
Explanation: The component containing vertices 0, 1, and 2 is complete since there is an edge between every pair of two vertices. On the other hand, the component containing vertices 3, 4, and 5 is not complete since there is no edge between vertices 4 and 5. Thus, the number of complete components in this graph is 1.

Constraints:

• 1 <= n <= 50
• 0 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 2
• 0 <= ai, bi <= n - 1
• ai != bi
• There are no repeated edges.

Solution

struct UnionSet {
  vector<int> parent;
public:
  UnionSet(int size): parent(size) {
    iota(parent.begin(), parent.end(), 0);
  }

  int find(int x) {
    if(parent[x] != x) parent[x] = find(parent[x]);
    return parent[x];
  }

  void merge(int x, int y) {
    x = find(x);
    y = find(y);
    parent[x] = y;
  }
};
class Solution {
public:
  int countCompleteComponents(int n, vector<vector<int>>& edges) {
    UnionSet us(n);
    for(auto &e : edges) {
      us.merge(e[0], e[1]);
    }
    map<int, int> edgeOfComponent;
    map<int, set<int>> vertexOfComponent;
    for(int i = 0; i < n; ++i) {
      vertexOfComponent[us.find(i)].insert(i);
    }
    for(auto &e : edges) {
      edgeOfComponent[us.find(e[0])] += 1;
    }
    int answer = 0;
    for(auto [root, vertices] : vertexOfComponent) {
      int verticesCount = vertices.size();
      answer += (verticesCount * (verticesCount - 1) / 2 == edgeOfComponent[root]);
    }
    return answer;
  }
};

// Accepted
// 3355/3355 cases passed (65 ms)
// Your runtime beats 41.32 % of cpp submissions
// Your memory usage beats 67.11 % of cpp submissions (129.4 MB)