Today I have done leetcode's January LeetCoding Challenge with cpp.

January LeetCoding Challenge 30

Description

Divide Nodes Into the Maximum Number of Groups

You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.

You are also given a 2D integer array edges, where edges[i] = [ai, bi] indicates that there is a bidirectional edge between nodes ai and bi. Notice that the given graph may be disconnected.

Divide the nodes of the graph into m groups (1-indexed) such that:

• Each node in the graph belongs to exactly one group.
• For every pair of nodes in the graph that are connected by an edge [ai, bi], if ai belongs to the group with index x, and bi belongs to the group with index y, then |y - x| = 1.

Return the maximum number of groups (i.e., maximum m) into which you can divide the nodes. Return -1 if it is impossible to group the nodes with the given conditions.

Example 1:

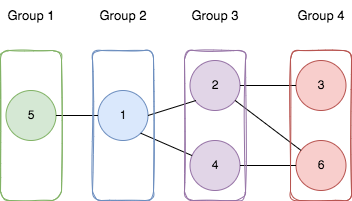
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
Output: 4
Explanation: As shown in the image we:
- Add node 5 to the first group.
- Add node 1 to the second group.
- Add nodes 2 and 4 to the third group.
- Add nodes 3 and 6 to the fourth group.
We can see that every edge is satisfied.
It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.

Example 2:

Input: n = 3, edges = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied.
It can be shown that no grouping is possible.

Constraints:

• 1 <= n <= 500
• 1 <= edges.length <= 104
• edges[i].length == 2
• 1 <= ai, bi <= n
• ai != bi
• There is at most one edge between any pair of vertices.

Solution

class Solution {
  bool isBipartite(vector<vector<int>> &neighbors, int current, vector<int> &color) {
    for(auto next : neighbors[current]) {
      if(color[next] == color[current]) return false;
      if(color[next] == -1) {
        color[next] = !color[current];
        if(!isBipartite(neighbors, next, color)) return false;
      }
    }
    return true;
  }

  int getLongestShortestPath(vector<vector<int>> &neighbors, int current, int n) {
    queue<int> q;
    vector<bool> visited(n);

    q.push(current);
    visited[current] = true;
    int distance = 0;

    while(q.size()) {
      int sz = q.size();
      for(int _ = 0; _ < sz; ++_) {
        int cur = q.front();
        q.pop();

        for(auto next : neighbors[cur]) {
          if(visited[next]) continue;
          visited[next] = true;
          q.push(next);
        }
      }
      distance += 1;
    }
    return distance;
  }
  int getGroups(vector<vector<int>> &neighbors, int current, vector<int> &distance, vector<bool> &visited) {
    int maxNumber = distance[current];
    visited[current] = true;

    for(auto next : neighbors[current]) {
      if(visited[next]) continue;
      maxNumber = max(maxNumber, getGroups(neighbors, next, distance, visited));
    }
    return maxNumber;
  }
public:
  int magnificentSets(int n, vector<vector<int>>& edges) {
    vector<vector<int>> neighbors(n);
    for(auto &e : edges) {
      neighbors[e[0] - 1].push_back(e[1] - 1);
      neighbors[e[1] - 1].push_back(e[0] - 1);
    }
    vector<int> color(n, -1);
    for(int i = 0; i < n; ++i) {
      if(color[i] != -1) continue;
      color[i] = 0;
      if(!isBipartite(neighbors, i, color)) return -1;
    }

    vector<int> distance(n);
    for(int i = 0; i < n; ++i) {
      distance[i] = getLongestShortestPath(neighbors, i, n);
    }

    int answer = 0;
    vector<bool> visited(n);
    for(int i = 0; i < n; ++i) {
      if(visited[i]) continue;
      answer += getGroups(neighbors, i, distance, visited);
    }
    return answer;
  }
};

// Accepted
// 55/55 cases passed (143 ms)
// Your runtime beats 65.55 % of cpp submissions
// Your memory usage beats 90.76 % of cpp submissions (41.6 MB)