Today I have done leetcode's January LeetCoding Challenge with cpp.

January LeetCoding Challenge 18

Description

Minimum Cost to Make at Least One Valid Path in a Grid

Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:

• 1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
• 2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
• 3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
• 4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])

Notice that there could be some signs on the cells of the grid that point outside the grid.

You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.

You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.

Return the minimum cost to make the grid have at least one valid path.

Example 1:

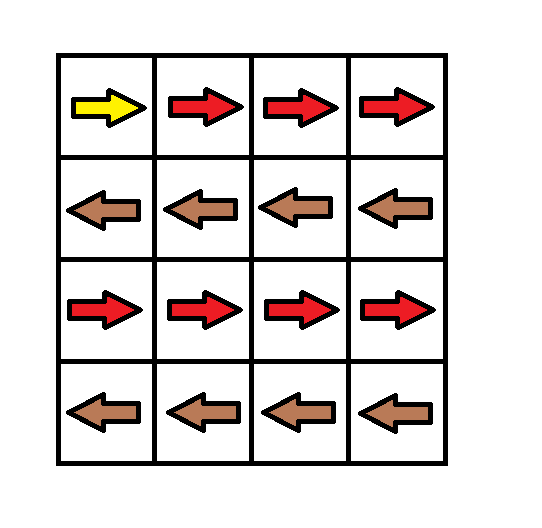
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.

Example 2:

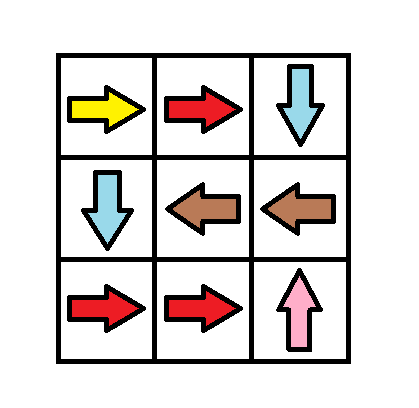
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).

Example 3:

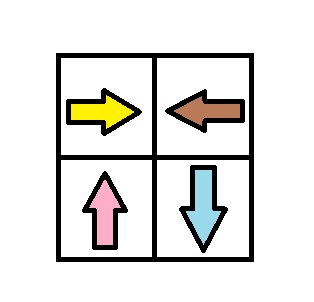
Input: grid = [[1,2],[4,3]]
Output: 1

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• 1 <= grid[i][j] <= 4

Solution

class Solution {
  const int MOVES[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
  using pi = pair<int, int>;
public:
  int minCost(vector<vector<int>>& grid) {
    int rows = grid.size();
    int cols = grid.front().size();
    vector<vector<pi>> neighbors(rows * cols);
    for(int i = 0; i < rows; ++i) {
      for(int j = 0; j < cols; ++j) {
        int pos = i * cols + j;
        for(int m = 0; m < 4; ++m) {
          int newRow = i + MOVES[m][0];
          int newCol = j + MOVES[m][1];
          if(newRow < 0 || newCol < 0 || newRow >= rows || newCol >= cols) continue;
          int newPos = newRow * cols + newCol;
          neighbors[pos].push_back({newPos, grid[i][j] != m + 1});
        }
      }
    }
    priority_queue<pi, vector<pi>, greater<pi>> pq;
    pq.push({0, 0});
    set<int> visited;
    while(pq.size()) {
      auto [cost, pos] = pq.top();
      pq.pop();
      if(pos == rows * cols - 1) return cost;
      if(visited.count(pos)) continue;
      visited.insert(pos);
      for(auto [next, moveCost] : neighbors[pos]) {
        pq.push({cost + moveCost, next});
      }
    }
    return -1;
  }
};

// Accepted
// 69/69 cases passed (173 ms)
// Your runtime beats 9 % of cpp submissions
// Your memory usage beats 13.65 % of cpp submissions (46.7 MB)