Today I have done leetcode's December LeetCoding Challenge with cpp.

December LeetCoding Challenge 21

Description

Maximum Number of K-Divisible Components

There is an undirected tree with n nodes labeled from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

You are also given a 0-indexed integer array values of length n, where values[i] is the value associated with the ith node, and an integer k.

A valid split of the tree is obtained by removing any set of edges, possibly empty, from the tree such that the resulting components all have values that are divisible by k, where the value of a connected component is the sum of the values of its nodes.

Return the maximum number of components in any valid split.

Example 1:

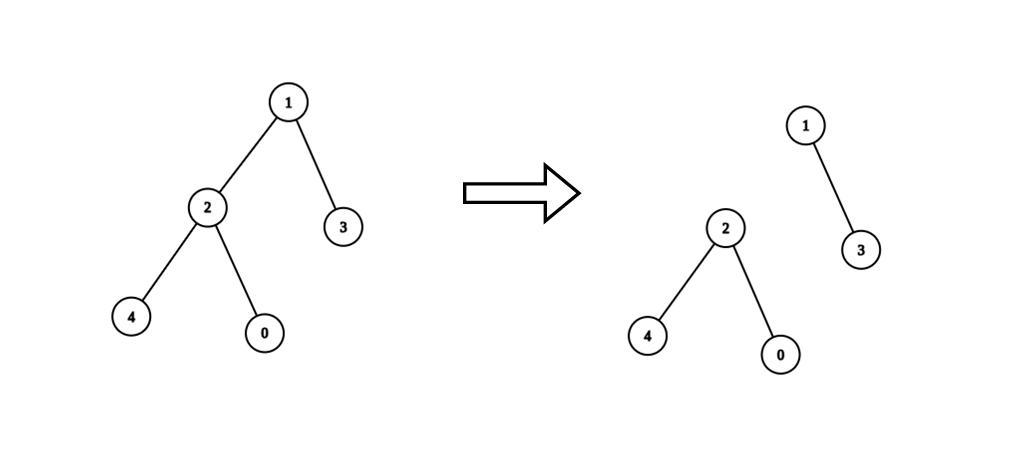
Input: n = 5, edges = [[0,2],[1,2],[1,3],[2,4]], values = [1,8,1,4,4], k = 6
Output: 2
Explanation: We remove the edge connecting node 1 with 2. The resulting split is valid because:
- The value of the component containing nodes 1 and 3 is values[1] + values[3] = 12.
- The value of the component containing nodes 0, 2, and 4 is values[0] + values[2] + values[4] = 6.
It can be shown that no other valid split has more than 2 connected components.

Example 2:

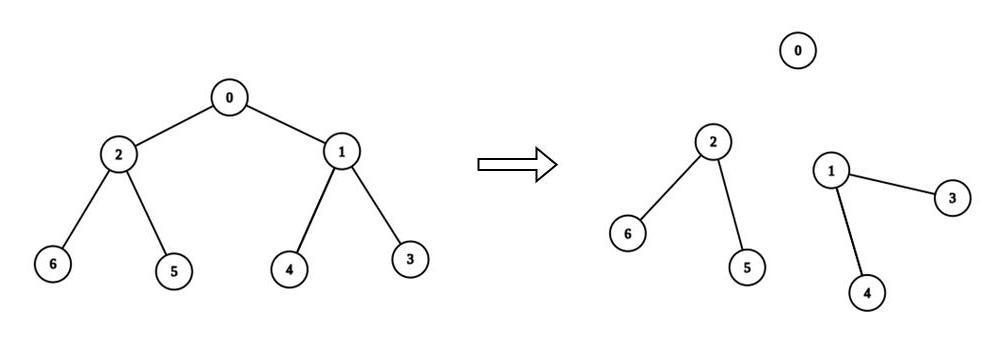
Input: n = 7, edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]], values = [3,0,6,1,5,2,1], k = 3
Output: 3
Explanation: We remove the edge connecting node 0 with 2, and the edge connecting node 0 with 1. The resulting split is valid because:
- The value of the component containing node 0 is values[0] = 3.
- The value of the component containing nodes 2, 5, and 6 is values[2] + values[5] + values[6] = 9.
- The value of the component containing nodes 1, 3, and 4 is values[1] + values[3] + values[4] = 6.
It can be shown that no other valid split has more than 3 connected components.

Constraints:

• 1 <= n <= 3 * 104
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• values.length == n
• 0 <= values[i] <= 109
• 1 <= k <= 109
• Sum of values is divisible by k.
• The input is generated such that edges represents a valid tree.

Solution

class Solution {
public:
  int maxKDivisibleComponents(int n, vector<vector<int>>& edges, vector<int>& values, int k) {
    vector<vector<int>> graph(n);
    vector<int> degree(n);

    if(n < 2) return 1;
    for(const auto &e : edges) {
      graph[e[0]].push_back(e[1]);
      graph[e[1]].push_back(e[0]);
      degree[e[0]] += 1;
      degree[e[1]] += 1;
    }

    vector<long long> nodeVals(values.begin(), values.end());
    queue<int> q;
    for(int i = 0; i < n; ++i) {
      if(degree[i] == 1) q.push(i);
    }

    int answer = 0;
    while(q.size()) {
      int cur = q.front();
      q.pop();
      degree[cur] -= 1;
      long long carry = 0;
      if(nodeVals[cur] % k == 0) answer += 1;
      else carry = nodeVals[cur];
      for(int next : graph[cur]) {
        if(degree[next] == 0) continue;
        degree[next] -= 1;
        nodeVals[next] += carry;
        if(degree[next] == 1) q.push(next);
      }
    }

    return answer;
  }
};

// Accepted
// 736/736 cases passed (90 ms)
// Your runtime beats 93.67 % of cpp submissions
// Your memory usage beats 67.09 % of cpp submissions (176.1 MB)