Today I have done leetcode's August LeetCoding Challenge with cpp.

August LeetCoding Challenge 9

Description

Magic Squares In Grid

A 3 x 3 magic square is a 3 x 3 grid filled with distinct numbers from 1 to 9 such that each row, column, and both diagonals all have the same sum.

Given a row x col grid of integers, how many 3 x 3 contiguous magic square subgrids are there?

Note: while a magic square can only contain numbers from 1 to 9, grid may contain numbers up to 15.

Example 1:

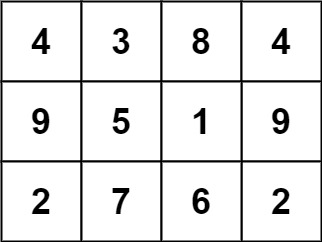
Input: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]]
Output: 1
Explanation: 
The following subgrid is a 3 x 3 magic square:

while this one is not:

In total, there is only one magic square inside the given grid.

Example 2:

Input: grid = [[8]]
Output: 0

Constraints:

• row == grid.length
• col == grid[i].length
• 1 <= row, col <= 10
• 0 <= grid[i][j] <= 15

Solution

class Solution {
  const int target = (1 << 10) - 2;
public:
  int numMagicSquaresInside(vector<vector<int>>& grid) {
    int rows = grid.size();
    int cols = grid.front().size();
    int answer = 0;
    for(int i = 0; i <= rows - 3; ++i) {
      for(int j = 0; j <= cols - 3; ++j) {
        int result = 0;
        for(int ii = 0; ii < 3; ++ii) {
          for(int jj = 0; jj < 3; ++jj) {
            result |= (1 << grid[i + ii][j + jj]);
          }
        }
        if(result != target) continue;
        bool ok = true;
        int sum = grid[i][j] + grid[i][j + 1] + grid[i][j + 2];
        for(int ii = 0; ii < 3; ++ii) {
          if(grid[i + ii][j] + grid[i + ii][j + 1] + grid[i + ii][j + 2] != sum) ok = false;
          if(grid[i][j + ii] + grid[i + 1][j + ii] + grid[i + 2][j + ii] != sum) ok = false;
        }
        if(grid[i][j] + grid[i + 1][j + 1] + grid[i + 2][j + 2] != sum) ok = false;
        if(grid[i][j + 2] + grid[i + 1][j + 1] + grid[i + 2][j] != sum) ok = false;
        answer += ok;
      }
    }
    return answer;
  }
};