Today I have done leetcode's February LeetCoding Challenge with cpp.

February LeetCoding Challenge 11

Description

Cherry Pickup II

You are given a rows x cols matrix grid representing a field of cherries where grid[i][j] represents the number of cherries that you can collect from the (i, j) cell.

You have two robots that can collect cherries for you:

Robot #1 is located at the top-left corner (0, 0), and
Robot #2 is located at the top-right corner (0, cols - 1).

Return the maximum number of cherries collection using both robots by following the rules below:

From a cell (i, j), robots can move to cell (i + 1, j - 1), (i + 1, j), or (i + 1, j + 1).
When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
When both robots stay in the same cell, only one takes the cherries.
Both robots cannot move outside of the grid at any moment.
Both robots should reach the bottom row in grid.

Example 1:

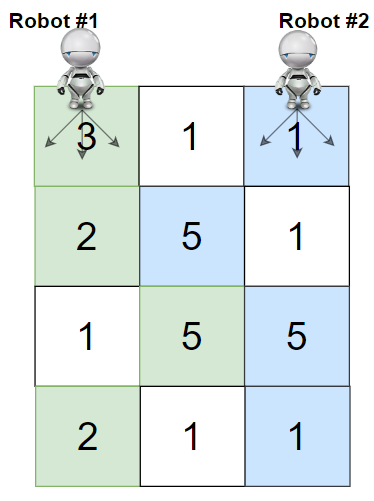
Input: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
Output: 24
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.

Example 2:

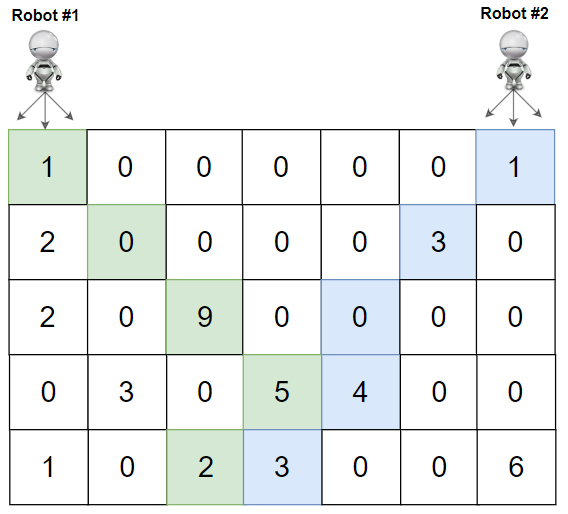
Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
Output: 28
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.

Constraints:

rows == grid.length
cols == grid[i].length
2 <= rows, cols <= 70
0 <= grid[i][j] <= 100

Solution

auto speedup = [](){
  cin.tie(nullptr);
  cout.tie(nullptr);
  ios::sync_with_stdio(false);
  return 0;
}();
const int moves[9][2] = {
  {-1, -1},
  {-1, 0},
  {-1, 1},
  {0, -1},
  {0, 0},
  {0, 1},
  {1, -1},
  {1, 0},
  {1, 1},
};
class Solution {
public:
  int cherryPickup(vector<vector<int>>& grid) {
    int rows = grid.size();
    int cols = grid.front().size();
    // col1 * cols + col2
    int dp[2][cols * cols];
    memset(dp, -1, sizeof(dp));
    // 0 * cols + cols - 1
    dp[0][cols - 1] = grid[0][0] + grid[0][cols - 1];
    for(int row = 0; row < rows - 1; ++row) {
      int parity = (row & 1);
      for(int index = 0; index < cols * cols; ++index) {
        if(dp[parity][index] == -1) continue;
        int col1 = index / cols;
        int col2 = index % cols;
        for(int m = 0 ; m < 9; ++m) {
          int newCol1 = col1 + moves[m][0];
          int newCol2 = col2 + moves[m][1];
          int newIndex = newCol1 * cols + newCol2;
          if(newCol1 < 0 || newCol2 < 0 || newCol1 >= cols || newCol2 >= cols) continue;
          if(newCol1 > newCol2) continue;
          int cherries = grid[row + 1][newCol1];
          if(newCol2 != newCol1) {
            cherries += grid[row + 1][newCol2];
          }
          dp[parity ^ 1][newIndex] = max(dp[parity ^ 1][newIndex], dp[parity][index] + cherries);
        }
      }
    }
    auto resultSet = dp[((rows & 1) ^ 1)];
    int answer = *max_element(resultSet, resultSet + cols * cols);
    return answer;
  }
};

// Accepted
// 59/59 cases passed (19 ms)
// Your runtime beats 99.56 % of cpp submissions
// Your memory usage beats 83.8 % of cpp submissions (11.1 MB)

2024-02-11 Daily Challenge

February LeetCoding Challenge 11

Description

Solution