Today I have done leetcode's November LeetCoding Challenge with cpp.

November LeetCoding Challenge 11

Description

Design Graph With Shortest Path Calculator

There is a directed weighted graph that consists of n nodes numbered from 0 to n - 1. The edges of the graph are initially represented by the given array edges where edges[i] = [fromi, toi, edgeCosti] meaning that there is an edge from fromi to toi with the cost edgeCosti.

Implement the Graph class:

• Graph(int n, int[][] edges) initializes the object with n nodes and the given edges.
• addEdge(int[] edge) adds an edge to the list of edges where edge = [from, to, edgeCost]. It is guaranteed that there is no edge between the two nodes before adding this one.
• int shortestPath(int node1, int node2) returns the minimum cost of a path from node1 to node2. If no path exists, return -1. The cost of a path is the sum of the costs of the edges in the path.

Example 1:

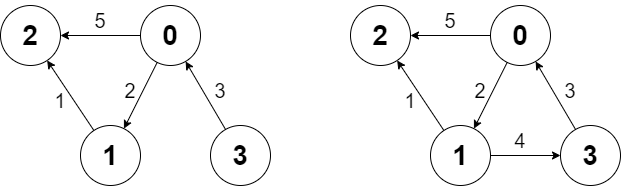
Input
["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"]
[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]]
Output
[null, 6, -1, null, 6]
Explanation
Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);
g.shortestPath(3, 2); // return 6. The shortest path from 3 to 2 in the first diagram above is 3 -> 0 -> 1 -> 2 with a total cost of 3 + 2 + 1 = 6.
g.shortestPath(0, 3); // return -1. There is no path from 0 to 3.
g.addEdge([1, 3, 4]); // We add an edge from node 1 to node 3, and we get the second diagram above.
g.shortestPath(0, 3); // return 6. The shortest path from 0 to 3 now is 0 -> 1 -> 3 with a total cost of 2 + 4 = 6.

Constraints:

• 1 <= n <= 100
• 0 <= edges.length <= n * (n - 1)
• edges[i].length == edge.length == 3
• 0 <= fromi, toi, from, to, node1, node2 <= n - 1
• 1 <= edgeCosti, edgeCost <= 106
• There are no repeated edges and no self-loops in the graph at any point.
• At most 100 calls will be made for addEdge.
• At most 100 calls will be made for shortestPath.

Solution

class Graph {
  using pi = pair<int, int>;
  vector<vector<pi>> adjacencyList;
  int sz;
public:
  Graph(int n, vector<vector<int>>& edges): sz(n) {
    adjacencyList.resize(n);
    for(const auto &edge : edges) {
      adjacencyList[edge[0]].push_back({edge[1], edge[2]});
    }
  }
  
  void addEdge(vector<int> edge) {
    adjacencyList[edge[0]].push_back({edge[1], edge[2]});
  }
  
  int shortestPath(int node1, int node2) {
    vector<int> dist(sz, INT_MAX);
    priority_queue<pi, vector<pi>, greater<pi>> pq;

    pq.push({0, node1});
    while(pq.size()) {
      auto [d, current] = pq.top();
      pq.pop();
      if(current == node2) return d;
      if(dist[current] != INT_MAX) continue;
      dist[current] = d;

      for(const auto &[next, cost] : adjacencyList[current]) {
        if(dist[next] != INT_MAX) continue;
        pq.push({d + cost, next});
      }
    }

    return -1;
  }
};

// Accepted
// 36/36 cases passed (194 ms)
// Your runtime beats 74.79 % of cpp submissions
// Your memory usage beats 15.41 % of cpp submissions (113.4 MB)