2023-09-15 Daily Challenge

Posted on:
Posted modified:
In: DailyChallenge

Today I have done leetcode's September LeetCoding Challenge with cpp.

September LeetCoding Challenge 15

Description

Min Cost to Connect All Points

You are given an array points representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].

The cost of connecting two points [xi, yi] and [xj, yj] is the manhattan distance between them: |xi - xj| + |yi - yj|, where |val| denotes the absolute value of val.

Return the minimum cost to make all points connected. All points are connected if there is exactly one simple path between any two points.

 

Example 1:

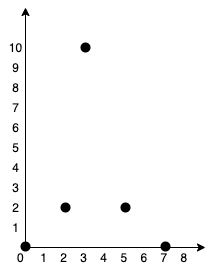
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20
Explanation: 

We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.

Example 2:

Input: points = [[3,12],[-2,5],[-4,1]]
Output: 18

 

Constraints:

  • 1 <= points.length <= 1000
  • -106 <= xi, yi <= 106
  • All pairs (xi, yi) are distinct.

Solution

auto speedup = [](){
  cin.tie(nullptr);
  cout.tie(nullptr);
  ios::sync_with_stdio(false);
  return 0;
}();
class Solution {
  using pi = pair<int, int>;
public:
  int minCostConnectPoints(vector<vector<int>>& points) {
    int len = points.size();
    vector<bool> connected(len);
    priority_queue<pi, vector<pi>, greater<pi>> pq;
    connected[0] = true;
    for(int i = 1; i < len; ++i) {
      pq.push({abs(points[i][0] - points[0][0]) + abs(points[i][1] - points[0][1]), i});
    }
    int answer = 0;
    int rest = len - 1;
    while(pq.size() && rest) {
      auto [cost, point] = pq.top();
      pq.pop();
      if(connected[point]) continue;
      connected[point] = true;
      answer += cost;
      rest -= 1;
      for(int i = 1; i < len; ++i) {
        if(connected[i]) continue;
        pq.push({abs(points[i][0] - points[point][0]) + abs(points[i][1] - points[point][1]), i});
      }
    }
    return answer;
  }
};

// Accepted
// 72/72 cases passed (136 ms)
// Your runtime beats 84.36 % of cpp submissions
// Your memory usage beats 77.28 % of cpp submissions (42.6 MB)
Algorithm