Today I have done leetcode's February LeetCoding Challenge with cpp.

February LeetCoding Challenge 12

Description

Minimum Fuel Cost to Report to the Capital

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of n cities numbered from 0 to n - 1 and exactly n - 1 roads. The capital city is city 0. You are given a 2D integer array roads where roads[i] = [ai, bi] denotes that there exists a bidirectional road connecting cities ai and bi.

There is a meeting for the representatives of each city. The meeting is in the capital city.

There is a car in each city. You are given an integer seats that indicates the number of seats in each car.

A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel.

Return the minimum number of liters of fuel to reach the capital city.

Example 1:

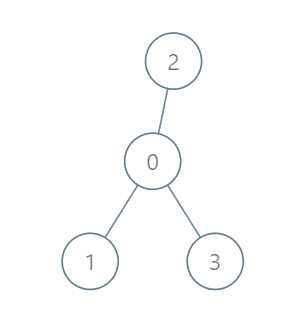
Input: roads = [[0,1],[0,2],[0,3]], seats = 5
Output: 3
Explanation: 
- Representative1 goes directly to the capital with 1 liter of fuel.
- Representative2 goes directly to the capital with 1 liter of fuel.
- Representative3 goes directly to the capital with 1 liter of fuel.
It costs 3 liters of fuel at minimum. 
It can be proven that 3 is the minimum number of liters of fuel needed.

Example 2:

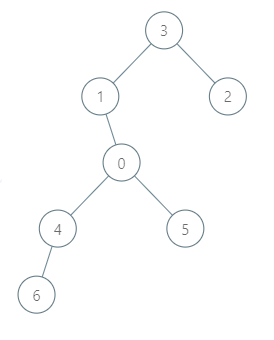
Input: roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
Output: 7
Explanation: 
- Representative2 goes directly to city 3 with 1 liter of fuel.
- Representative2 and representative3 go together to city 1 with 1 liter of fuel.
- Representative2 and representative3 go together to the capital with 1 liter of fuel.
- Representative1 goes directly to the capital with 1 liter of fuel.
- Representative5 goes directly to the capital with 1 liter of fuel.
- Representative6 goes directly to city 4 with 1 liter of fuel.
- Representative4 and representative6 go together to the capital with 1 liter of fuel.
It costs 7 liters of fuel at minimum. 
It can be proven that 7 is the minimum number of liters of fuel needed.

Example 3:

Input: roads = [], seats = 1
Output: 0
Explanation: No representatives need to travel to the capital city.

Constraints:

• 1 <= n <= 105
• roads.length == n - 1
• roads[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• roads represents a valid tree.
• 1 <= seats <= 105

Solution

class Solution {
  long long answer = 0;
  long long dfs(
    int current,
    int parrent,
    int seats,
    vector<vector<int>> &neighbors
  ) {
    int rep = 1;
    for(const auto next : neighbors[current]) {
      if(next == parrent) continue;
      rep += dfs(next, current, seats, neighbors);
    }
    if(current) {
      answer += (rep + seats - 1) / seats;
    }
    return rep;
  }
public:
  long long minimumFuelCost(vector<vector<int>>& roads, int seats) {
    if(roads.empty()) return 0;
    vector<vector<int>> neighbors(roads.size() + 1);
    for(const auto &road : roads) {
      neighbors[road[0]].push_back(road[1]);
      neighbors[road[1]].push_back(road[0]);
    }

    dfs(0, -1, seats, neighbors);
    return answer;
  }
};

// Accepted
// 131/131 cases passed (557 ms)
// Your runtime beats 98.46 % of cpp submissions
// Your memory usage beats 77.66 % of cpp submissions (191.4 MB)