Today I have done leetcode's January LeetCoding Challenge with cpp.

January LeetCoding Challenge 11

Description

Minimum Time to Collect All Apples in a Tree

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.

Example 1:

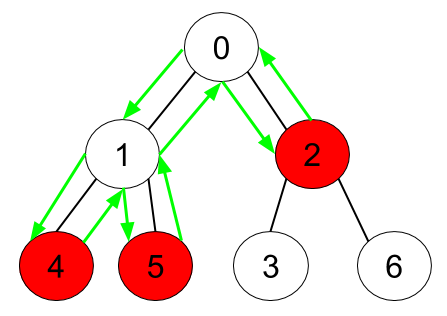
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8 
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 2:

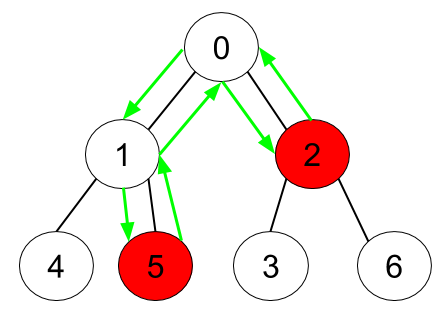
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.  

Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

Constraints:

• 1 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai < bi <= n - 1
• fromi < toi
• hasApple.length == n

Solution

class Solution {
  vector<bool> hasApple;
  vector<vector<int>> neighbors;
  
  bool constructTree(int current, int parrent, vector<bool>& isApple) {
    bool hasApple = isApple[current];
    for(auto next : neighbors[current]) {
      if(next == parrent) continue;
      hasApple = constructTree(next, current, isApple) || hasApple;
    }
    this->hasApple[current] = hasApple;
    return hasApple;
  }
public:
  int minTime(int n, vector<vector<int>>& edges, vector<bool>& isApple) {
    hasApple.resize(n);
    neighbors.resize(n);
    for(const auto &edge : edges) {
      neighbors[edge[0]].push_back(edge[1]);
      neighbors[edge[1]].push_back(edge[0]);
    }
    constructTree(0, -1, isApple);
    if(!hasApple[0]) return 0;
    queue<pair<int, int>> q;
    q.push({0, -1});
    int answer = 0;
    while(q.size()) {
      auto [current, parrent] = q.front();
      q.pop();
      for(auto next : neighbors[current]) {
        if(next == parrent) continue;
        if(!hasApple[next]) continue;
        answer += 2;
        q.push({next, current});
      }
    }
    return answer;
  }
};

// Accepted
// 55/55 cases passed (189 ms)
// Your runtime beats 86.24 % of cpp submissions
// Your memory usage beats 50 % of cpp submissions (61.3 MB)