Today I have done leetcode's December LeetCoding Challenge with cpp.

December LeetCoding Challenge 10

Description

Maximum Product of Splitted Binary Tree

Given the root of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.

Return the maximum product of the sums of the two subtrees. Since the answer may be too large, return it modulo 109 + 7.

Note that you need to maximize the answer before taking the mod and not after taking it.

Example 1:

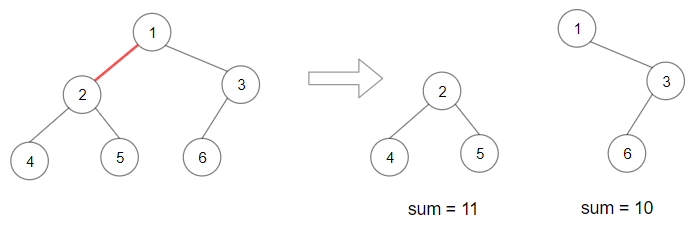
Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)

Example 2:

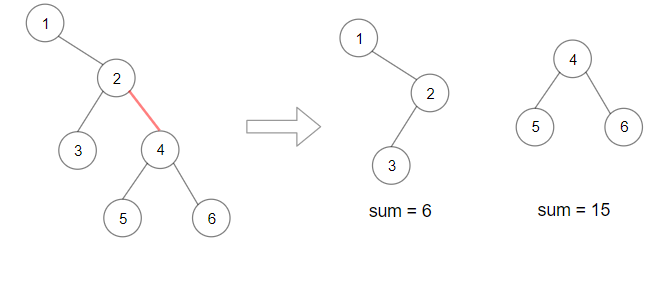
Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation: Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)

Constraints:

• The number of nodes in the tree is in the range [2, 5 * 104].
• 1 <= Node.val <= 104

Solution

auto speedup = [](){
  cin.tie(nullptr);
  cout.tie(nullptr);
  ios::sync_with_stdio(false);
  return 0;
}();
const int MOD = 1e9 + 7;
class Solution {
  int sum = 0;
  int cur = 0;
  void add(TreeNode *root) {
    if(!root) return;
    sum += root->val;
    add(root->left);
    add(root->right);
  }
  int solve(TreeNode *root) {
    if(!root) return 0;
    int left = solve(root->left);
    int right = solve(root->right);
    if(abs(left + right + root->val - sum / 2) < abs(cur - sum / 2)) {
      cur = left + right + root->val;
    }
    if (abs(left - sum / 2) < abs(cur - sum / 2)) {
      cur = left;
    }
    if (abs(right - sum / 2) < abs(cur - sum / 2)) {
      cur = right;
    }
    return left + right + root->val;
  }
public:
  int maxProduct(TreeNode* root) {
    add(root);
    solve(root);
    return 1LL * (sum - cur) * cur % MOD;
  }
};

// Accepted
// 54/54 cases passed (84 ms)
// Your runtime beats 100 % of cpp submissions
// Your memory usage beats 63.53 % of cpp submissions (77.5 MB)