2022-04-28 Daily-Challenge

Posted on:
Posted modified:
In: DailyChallenge
|

Today I have done leetcode's April LeetCoding Challenge with cpp.

April LeetCoding Challenge 28

Description

Path With Minimum Effort

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1:

img

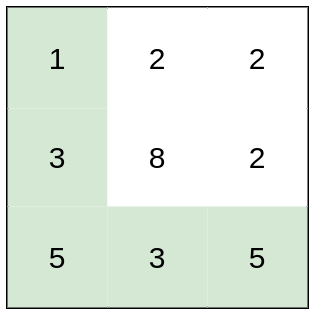
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

img

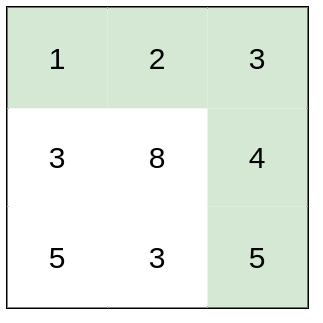
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

img

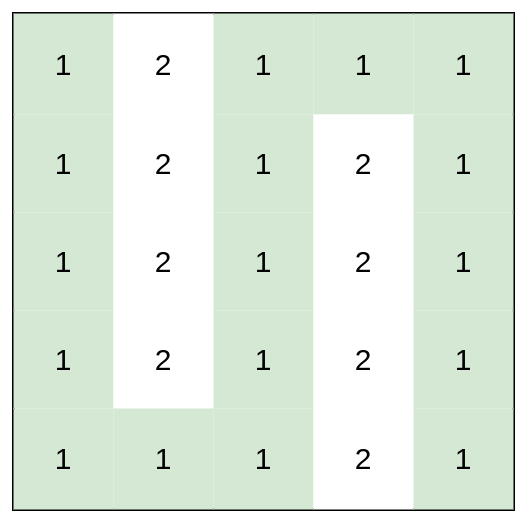
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

Constraints:

  • rows == heights.length
  • columns == heights[i].length
  • 1 <= rows, columns <= 100
  • 1 <= heights[i][j] <= 10^6

Solution

auto speedup = []() {
  cin.tie(nullptr);
  cout.tie(nullptr);
  ios::sync_with_stdio(false);
  return 0;
}();

using pi = pair<int, int>;
bool vis[2][100][100];
int efforts[2][100][100];
class Solution {
  int moves[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
public:
  int minimumEffortPath(vector<vector<int>>& heights) {
    memset(vis, 0, sizeof(vis));
    int rows = heights.size();
    int cols = heights.front().size();
    priority_queue<pi, vector<pi>, greater<pi>> q[2];
    q[0].push({0, 0});
    q[1].push({0, rows * cols - 1});
    while(true) {
      for(int parity = 0; parity < 2; ++parity) {
        while(q[parity].size()) {
          auto [effort, pos] = q[parity].top();
          q[parity].pop();
          int row = pos / cols;
          int col = pos % cols;
          if(vis[!parity][row][col]) return max(effort, efforts[!parity][row][col]);
          if(vis[parity][row][col]) continue;
          vis[parity][row][col] = true;
          efforts[parity][row][col] = effort;
          for(int i = 0; i < 4; ++i) {
            int newRow = row + moves[i][0];
            int newCol = col + moves[i][1];
            if(newRow < 0 || newCol < 0 || newRow >= rows || newCol >= cols) continue;
            if(vis[parity][newRow][newCol]) continue;
            q[parity].push({max(effort, abs(heights[newRow][newCol] - heights[row][col])), newRow * cols + newCol});
          }
          break;
        }
      }
    }
    return -1;
  }
};

// Accepted
// 75/75 cases passed (36 ms)
// Your runtime beats 100 % of cpp submissions
// Your memory usage beats 93.52 % of cpp submissions (16.8 MB)
Algorithm