2021-11-24 Daily-Challenge

Posted on:
Posted modified:
In: DailyChallenge

Today I have done leetcode's November LeetCoding Challenge with cpp.

November LeetCoding Challenge 24

Description

Interval List Intersections

You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [starti, endi] and secondList[j] = [startj, endj]. Each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

A closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.

The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].

Example 1:

img

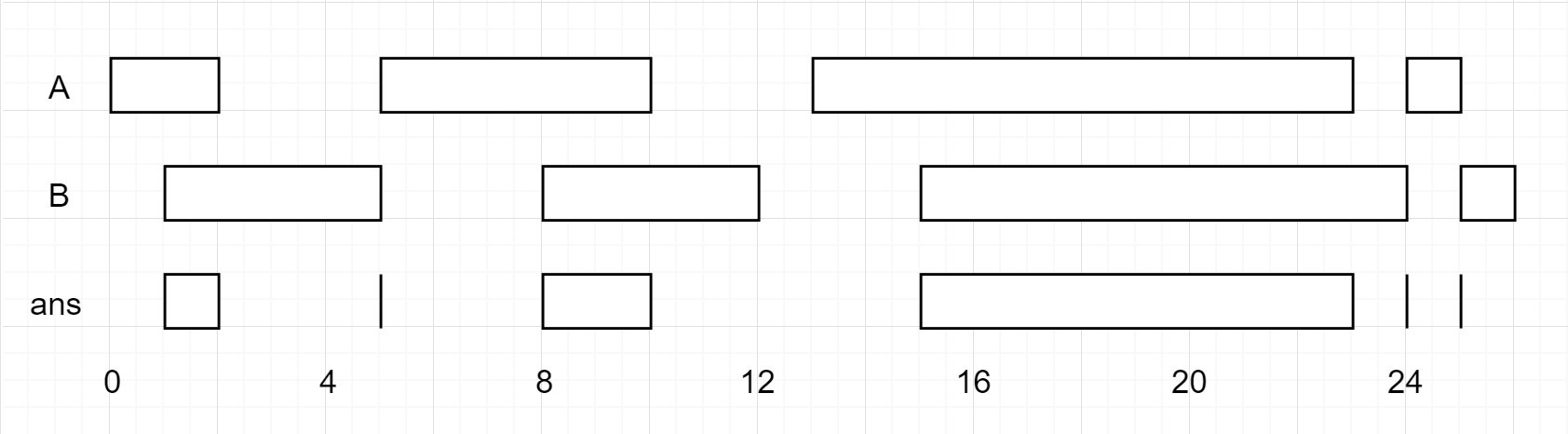
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

Example 2:

Input: firstList = [[1,3],[5,9]], secondList = []
Output: []

Example 3:

Input: firstList = [], secondList = [[4,8],[10,12]]
Output: []

Example 4:

Input: firstList = [[1,7]], secondList = [[3,10]]
Output: [[3,7]]

Constraints:

  • 0 <= firstList.length, secondList.length <= 1000
  • firstList.length + secondList.length >= 1
  • 0 <= starti < endi <= 109
  • endi < starti+1
  • 0 <= startj < endj <= 109
  • endj < startj+1

Solution

auto speedup = [](){
  cin.tie(nullptr);
  cout.tie(nullptr);
  ios::sync_with_stdio(false);
  return 0;
}();
class Solution {
public:
  vector<vector<int>> intervalIntersection(vector<vector<int>>& firstList, vector<vector<int>>& secondList) {
    auto it1 = firstList.begin();
    auto end1 = firstList.end();
    auto it2 = secondList.begin();
    auto end2 = secondList.end();
    vector<vector<int>> answer;
    while(it1 != end1 && it2 != end2) {
      int begin = max((*it1)[0], (*it2)[0]);
      int end = min((*it1)[1], (*it2)[1]);
      if(end >= begin) {
        answer.push_back({begin, end});
      }
      if(end == (*it1)[1]) ++it1;
      if(end == (*it2)[1]) ++it2;
    }
    return answer;
  }
};

// Accepted
// 85/85 cases passed (24 ms)
// Your runtime beats 98.21 % of cpp submissions
// Your memory usage beats 75.13 % of cpp submissions (18.6 MB)
Algorithm