2021-09-06 Daily-Challenge
Today I have done Checking Existence of Edge Length Limited Paths and leetcode's September LeetCoding Challenge with cpp.
Checking Existence of Edge Length Limited Paths
Description
An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [ui, vi, disi] denotes an edge between nodes ui and vi with distance disi. Note that there may be multiple edges between two nodes.
Given an array queries, where queries[j] = [pj, qj, limitj], your task is to determine for each queries[j] whether there is a path between pj and qj such that each edge on the path has a distance strictly less than limitj .
Return a boolean array answer, where answer.length == queries.length and the jth value of answer is true if there is a path for queries[j] is true, and false otherwise.
Example 1:
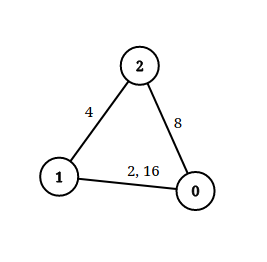
Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
Output: [false,true]
Explanation: The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.
Example 2:
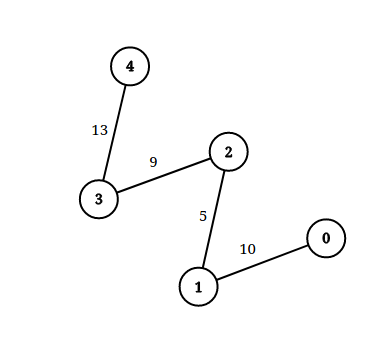
Input: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
Output: [true,false]
Exaplanation: The above figure shows the given graph.
Constraints:
2 <= n <= 1051 <= edgeList.length, queries.length <= 105edgeList[i].length == 3queries[j].length == 30 <= ui, vi, pj, qj <= n - 1ui != vipj != qj1 <= disi, limitj <= 109- There may be multiple edges between two nodes.
Solution
I first wrote dijkstra, then TLE, so I figured out.
auto speedup = [](){
cin.tie(nullptr);
cout.tie(nullptr);
ios::sync_with_stdio(false);
return 0;
}();
class Solution {
vector<int> parent;
int curIndex;
void init(int n, vector<vector<int>>& edgeList) {
curIndex = 0;
sort(edgeList.begin(), edgeList.end(), [](const vector<int>& a, const vector<int>& b) {
return a[2] < b[2];
});
parent.resize(n);
for(int i = 0; i < n; ++i) {
parent[i] = i;
}
}
int find(int x) {
if(parent[x] != x) parent[x] = find(parent[x]);
return parent[x];
}
void merge(int x, int y) {
int px = find(x);
int py = find(y);
parent[px] = py;
}
void solveToLength(int len, vector<vector<int>>& edgeList) {
for(; curIndex < edgeList.size() && edgeList[curIndex][2] < len; ++curIndex) {
merge(edgeList[curIndex][1], edgeList[curIndex][0]);
}
}
public:
vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {
init(n, edgeList);
int len = queries.size();
vector<int> order(len);
vector<bool> answer(len);
for(int i = 0; i < len; ++i) {
order[i] = i;
}
sort(order.begin(), order.end(), [&](int a, int b) {
return queries[a][2] < queries[b][2];
});
for(auto i : order) {
solveToLength(queries[i][2], edgeList);
answer[i] = (find(queries[i][0]) == find(queries[i][1]));
}
return answer;
}
};
// Accepted
// 23/23 cases passed (476 ms)
// Your runtime beats 98.73 % of cpp submissions
// Your memory usage beats 84.81 % of cpp submissions (109.6 MB)
September LeetCoding Challenge 6
Description
Slowest Key
A newly designed keypad was tested, where a tester pressed a sequence of n keys, one at a time.
You are given a string keysPressed of length n, where keysPressed[i] was the ith key pressed in the testing sequence, and a sorted list releaseTimes, where releaseTimes[i] was the time the ith key was released. Both arrays are 0-indexed. The 0th key was pressed at the time 0, and every subsequent key was pressed at the exact time the previous key was released.
The tester wants to know the key of the keypress that had the longest duration. The ith keypress had a duration of releaseTimes[i] - releaseTimes[i - 1], and the 0th keypress had a duration of releaseTimes[0].
Note that the same key could have been pressed multiple times during the test, and these multiple presses of the same key may not have had the same duration.
Return the key of the keypress that had the longest duration. If there are multiple such keypresses, return the lexicographically largest key of the keypresses.
Example 1:
Input: releaseTimes = [9,29,49,50], keysPressed = "cbcd"
Output: "c"
Explanation: The keypresses were as follows:
Keypress for 'c' had a duration of 9 (pressed at time 0 and released at time 9).
Keypress for 'b' had a duration of 29 - 9 = 20 (pressed at time 9 right after the release of the previous character and released at time 29).
Keypress for 'c' had a duration of 49 - 29 = 20 (pressed at time 29 right after the release of the previous character and released at time 49).
Keypress for 'd' had a duration of 50 - 49 = 1 (pressed at time 49 right after the release of the previous character and released at time 50).
The longest of these was the keypress for 'b' and the second keypress for 'c', both with duration 20.
'c' is lexicographically larger than 'b', so the answer is 'c'.
Example 2:
Input: releaseTimes = [12,23,36,46,62], keysPressed = "spuda"
Output: "a"
Explanation: The keypresses were as follows:
Keypress for 's' had a duration of 12.
Keypress for 'p' had a duration of 23 - 12 = 11.
Keypress for 'u' had a duration of 36 - 23 = 13.
Keypress for 'd' had a duration of 46 - 36 = 10.
Keypress for 'a' had a duration of 62 - 46 = 16.
The longest of these was the keypress for 'a' with duration 16.
Constraints:
releaseTimes.length == nkeysPressed.length == n2 <= n <= 10001 <= releaseTimes[i] <= 10^9releaseTimes[i] < releaseTimes[i+1]keysPressedcontains only lowercase English letters.
Solution
auto speedup = [](){
cin.tie(nullptr);
cout.tie(nullptr);
ios::sync_with_stdio(false);
return 0;
}();
class Solution {
public:
char slowestKey(vector<int>& releaseTimes, string keysPressed) {
int len = releaseTimes.size();
int curTime = 0;
char answer = ' ';
int pressTime = 0;
for(int i = 0; i < len; ++i) {
if(releaseTimes[i] - curTime > pressTime || (releaseTimes[i] - curTime == pressTime && keysPressed[i] > answer)) {
pressTime = releaseTimes[i] - curTime;
answer = keysPressed[i];
}
curTime = releaseTimes[i];
}
return answer;
}
};
// Accepted
// 105/105 cases passed (4 ms)
// Your runtime beats 97.21 % of cpp submissions
// Your memory usage beats 22.91 % of cpp submissions (10.8 MB)