Today is Saturday, I gonna review the tasks I've done this week, and finish today's leetcode's September LeetCoding Challenge with cpp.

LeetCode Review

Erect the Fence

too easy to review

Unique Binary Search Trees II

too easy to review

Array Nesting

too easy to review

Majority Element II

too easy to review

Spiral Matrix III

too easy to review

Minimum Area Rectangle II

too easy to review

Largest Number At Least Twice of Others

too easy to review

Sorting the Sentence

too easy to review

Range Addition II

too easy to review

Find Minimum in Rotated Sorted Array

too easy to review

September LeetCoding Challenge 4

Description

Sum of Distances in Tree

There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given the integer n and the array edges where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

Return an array answer of length n where answer[i] is the sum of the distances between the ith node in the tree and all other nodes.

Example 1:

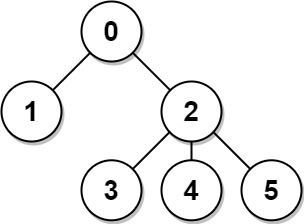
Input: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
Output: [8,12,6,10,10,10]
Explanation: The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer[0] = 8, and so on.

Example 2:

Input: n = 1, edges = []
Output: [0]

Example 3:

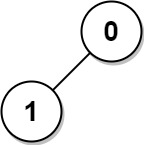
Input: n = 2, edges = [[1,0]]
Output: [1,1]

Constraints:

• 1 <= n <= 3 * 10^4
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• The given input represents a valid tree.

Solution

auto speedup = [](){
  cin.tie(nullptr);
  cout.tie(nullptr);
  ios::sync_with_stdio(false);
  return 0;
}();
class Solution {
  vector<int> dp, children, answer;
  vector<vector<int>> neighbors;
  
  void init(int N, vector<vector<int>>& edges) {
    dp.resize(N);
    children.resize(N, 1);
    answer.resize(N);
    neighbors.resize(N);
    
    for(auto &edge : edges) {
      neighbors[edge[0]].push_back(edge[1]);
      neighbors[edge[1]].push_back(edge[0]);
    }
  }
  
  void initDP(int current, int parent) {
    for(auto neighbor : neighbors[current]) {
      if(neighbor == parent) continue;
      
      initDP(neighbor, current);
      children[current] += children[neighbor];
      dp[current] += children[neighbor] + dp[neighbor];
    }
  }
  
  void swapRootDP(int current, int parent) {
    answer[current] = dp[current];
    
    for(auto neighbor : neighbors[current]) {
      if(neighbor == parent) continue;
      
      dp[current] -= children[neighbor] + dp[neighbor];
      children[current] -= children[neighbor];
      dp[neighbor] += dp[current] + children[current];
      children[neighbor] += children[current];
      
      swapRootDP(neighbor, current);
      dp[neighbor] -= dp[current] + children[current];
      children[neighbor] -= children[current];
      dp[current] += children[neighbor] + dp[neighbor];
      children[current] += children[neighbor];
    }
  }
public:
  vector<int> sumOfDistancesInTree(int N, vector<vector<int>>& edges) {
    init(N, edges);
    initDP(0, -1);
    swapRootDP(0, -1);
    return move(answer);
  }
};

// Accepted
// 73/73 cases passed (390 ms)
// Your runtime beats 11.33 % of cpp submissions
// Your memory usage beats 49.76 % of cpp submissions (87.4 MB)