Today is Sunday, I gonna review the tasks I've done this week, and finish today's leetcode's August LeetCoding Challenge with cpp.

LeetCode Review

Palindrome Partitioning II

auto speedup = [](){
  cin.tie(nullptr);
  cout.tie(nullptr);
  ios::sync_with_stdio(false);
  return 0;
}();
class Solution {
  bool isPalindrome(string &s, int start, int end) {
    while(start < end) {
      if(s[start++] != s[end--]) return false;
    }
    return true;
  }
public:
  int minCut(string s) {
    int len = s.length();
    if(isPalindrome(s, 0, len - 1)) return 0;
    for(int i = 1; i < len - 1; ++i) {
      if(isPalindrome(s, 0, i) && isPalindrome(s, i + 1, len - 1)) return 1;
    }
    vector<int> dp;
    dp.push_back(-1);
    for(int i = 0; i < len; ++i) {
      dp.push_back(i);
    }
    int pLen;
    for(int i = 0; i < len; ++i) {
      pLen = 0;
      while(i - pLen >= 0 && i + pLen < len && s[i - pLen] == s[i + pLen]) {
        dp[i + pLen + 1] = min(dp[i + pLen + 1], dp[i - pLen] + 1);
        pLen += 1;
      }
      pLen = 0;
      while(i - pLen >= 0 && i + pLen + 1 < len && s[i - pLen] == s[i + pLen + 1]) {
        dp[i + pLen + 2] = min(dp[i + pLen + 2], dp[i - pLen] + 1);
        pLen += 1;
      }
    }

    return dp.back();
  }
};
// Accepted
// 33/33 cases passed (0 ms)
// Your runtime beats 100 % of cpp submissions
// Your memory usage beats 87.96 % of cpp submissions (6.5 MB)

August LeetCoding Challenge 8

Description

Rank Transform of a Matrix

Given an m x n matrix, return a new matrix answer where answer[row][col] is the rank of matrix[row][col].

The rank is an integer that represents how large an element is compared to other elements. It is calculated using the following rules:

• The rank is an integer starting from 1.

• If two elements p and q are in the same row or column, then:

  • If p < q then rank(p) < rank(q)
  • If p == q then rank(p) == rank(q)
  • If p > q then rank(p) > rank(q)

• The rank should be as small as possible.

It is guaranteed that answer is unique under the given rules.

Example 1:

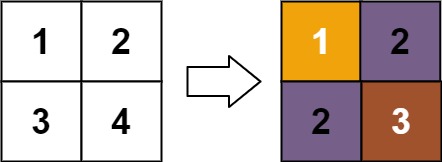
Input: matrix = [[1,2],[3,4]]
Output: [[1,2],[2,3]]
Explanation:
The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column.
The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2.

Example 2:

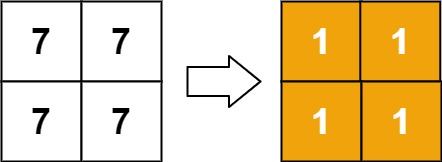
Input: matrix = [[7,7],[7,7]]
Output: [[1,1],[1,1]]

Example 3:

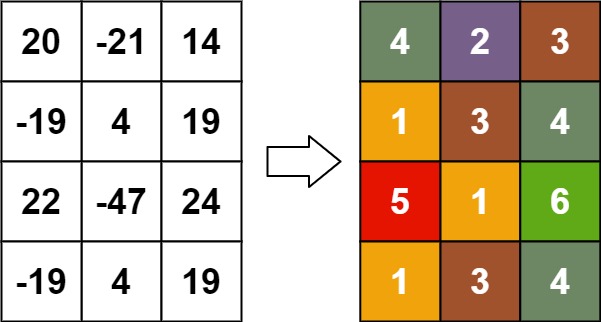
Input: matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
Output: [[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

Example 4:

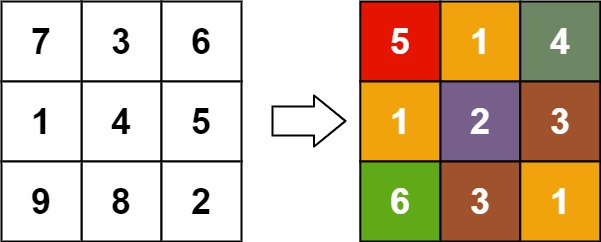
Input: matrix = [[7,3,6],[1,4,5],[9,8,2]]
Output: [[5,1,4],[1,2,3],[6,3,1]]

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 500
• -10^9 <= matrix[row][col] <= 10^9

Solution

auto speedup = [](){
  cin.tie(nullptr);
  cout.tie(nullptr);
  ios::sync_with_stdio(false);
  return 0;
}();
using pi = pair<int, int>;
class Solution {
  int rows;
  int cols;
  vector<int> parents;
  vector<int> maxRankInRow;
  vector<int> maxRankInCol;
  int find(int x) {
    if(parents[x] != x) parents[x] = find(parents[x]);
    return parents[x];
  }
  void merge(int x, int y) {
    int px = find(x);
    int py = find(y);
    parents[px] = parents[py];
  }

  void init(vector<vector<int>>& matrix) {
    rows = matrix.size();
    cols = matrix.front().size();
    maxRankInRow.resize(rows, INT_MIN);
    maxRankInCol.resize(cols, INT_MIN);
    parents.resize(rows + cols);
    vector<pi> vals;
    sort(vals.begin(), vals.end(), greater<pi>());
  }

  void solveVal(
    vector<vector<int>> &answer,
    vector<pi> &positions
  ) {
    for(int i = 0; i < rows + cols; ++i) {
      parents[i] = i;
    }
    for(auto [row, col] : positions) {
      merge(row, col + cols);
    }
    unordered_map<int, vector<pi>> groups;
    for(auto [row, col] : positions) {
      groups[find(row)].push_back({row, col});
    }

    for(auto &[_, group] : groups) {
      int rank = 1;
      for(auto [row, col] : group) {
        rank = max(rank, max(maxRankInRow[row], maxRankInCol[col]) + 1);
      }
      for(auto [row, col] : group) {
        answer[row][col] = rank;
        maxRankInCol[col] = max(rank, maxRankInCol[col]);
        maxRankInRow[row] = max(rank, maxRankInRow[row]);
      }
    }
  }
public:
  vector<vector<int>> matrixRankTransform(vector<vector<int>>& matrix) {
    init(matrix);
    priority_queue<pi, vector<pi>, greater<pi>> pq;
    for(int i = 0; i < rows; ++i) {
      for(int j = 0; j < cols; ++j) {
        pq.push({matrix[i][j], i * cols + j});
      }
    }

    vector<vector<int>> answer(rows, vector<int>(cols));
    vector<pi> sameVal;
    int prev = INT_MIN;
    while(pq.size()) {
      auto [val, pos] = pq.top();
      pq.pop();
      int row = pos / cols;
      int col = pos % cols;
      if(prev != val) {
        solveVal(answer, sameVal);
        sameVal.clear();
        prev = val;
      }
      sameVal.push_back({row, col});
    }
    solveVal(answer, sameVal);
    return answer;
  }
};

// Accepted
// 39/39 cases passed (344 ms)
// Your runtime beats 52.98 % of cpp submissions
// Your memory usage beats 82.09 % of cpp submissions (75.4 MB)