Today I have done Cinema Seat Allocation and leetcode's July LeetCoding Challenge with cpp.

Cinema Seat Allocation

Description

A cinema has n rows of seats, numbered from 1 to n and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.

Given the array reservedSeats containing the numbers of seats already reserved, for example, reservedSeats[i] = [3,8] means the seat located in row 3 and labelled with 8 is already reserved.

Return the maximum number of four-person groups you can assign on the cinema seats. A four-person group occupies four adjacent seats in one single row. Seats across an aisle (such as [3,3] and [3,4]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.

Example 1:

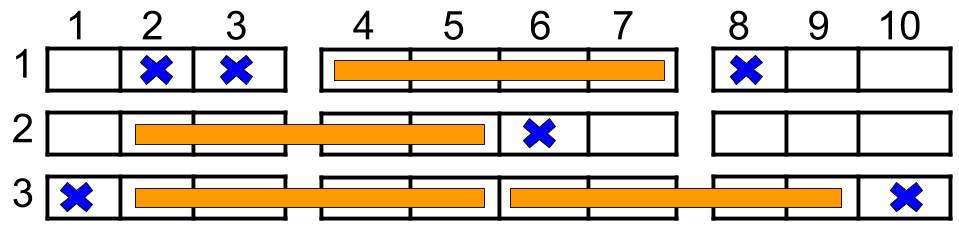
Input: n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]]
Output: 4
Explanation: The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.

Example 2:

Input: n = 2, reservedSeats = [[2,1],[1,8],[2,6]]
Output: 2

Example 3:

Input: n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]]
Output: 4

Constraints:

• 1 <= n <= 10^9
• 1 <= reservedSeats.length <= min(10*n, 10^4)
• reservedSeats[i].length == 2
• 1 <= reservedSeats[i][0] <= n
• 1 <= reservedSeats[i][1] <= 10
• All reservedSeats[i] are distinct.

Solution

auto speedup = [](){
  cin.tie(nullptr);
  cout.tie(nullptr);
  ios::sync_with_stdio(false);
  return 0;
}();
class Cashier {
  unordered_map<int, int> prices;
  int discountOrder;
  int orderCount = 0;
  double discount;
public:
  Cashier(int n, int discount, vector<int>& products, vector<int>& prices): discountOrder(n) {
    this->discount = (100 - discount) / 100.0;
    for(int i = 0; i < products.size(); ++i) {
      this->prices[products[i]] = prices[i];
    }
  }
  
  double getBill(vector<int> product, vector<int> amount) {
    double answer = 0;
    for(int i = 0; i < product.size(); ++i) {
      answer += prices[product[i]] * amount[i];
    }
    if(++orderCount % discountOrder == 0) {
      answer *= discount;
    }
    return answer;
  }
};

// Accepted
// 25/25 cases passed (172 ms)
// Your runtime beats 100 % of cpp submissions
// Your memory usage beats 95.6 % of cpp submissions (120.3 MB)

July LeetCoding Challenge 9

Description

Longest Increasing Subsequence

Given an integer array nums, return the length of the longest strictly increasing subsequence.

A subsequence is a sequence that can be derived from an array by deleting some or no elements without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7].

Example 1:

Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

Example 2:

Input: nums = [0,1,0,3,2,3]
Output: 4

Example 3:

Input: nums = [7,7,7,7,7,7,7]
Output: 1

Constraints:

• 1 <= nums.length <= 2500
• -104 <= nums[i] <= 104

Follow up: Can you come up with an algorithm that runs in O(n log(n)) time complexity?

Solution

auto speedup = [](){
  cin.tie(nullptr);
  cout.tie(nullptr);
  ios::sync_with_stdio(false);
  return 0;
}();
class Solution {
public:
  int lengthOfLIS(vector<int>& nums) {
    vector<int> LIS{nums[0]};
    for(auto i : nums) {
      auto it = lower_bound(LIS.begin(), LIS.end(), i);
      if(it != LIS.end()) {
        *it = i;
      } else {
        LIS.push_back(i);
      }
    }
    return LIS.size();
  }
};