Today I have done Frog Position After T Seconds and leetcode's July LeetCoding Challenge with cpp.

Frog Position After T Seconds

Description

Given an undirected tree consisting of n vertices numbered from 1 to n. A frog starts jumping from vertex 1. In one second, the frog jumps from its current vertex to another unvisited vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices, it jumps randomly to one of them with the same probability. Otherwise, when the frog can not jump to any unvisited vertex, it jumps forever on the same vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi.

Return the probability that after t seconds the frog is on the vertex target.

Example 1:

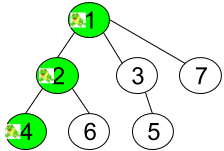
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
Output: 0.16666666666666666 
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after second 1 and then jumping with 1/2 probability to vertex 4 after second 2. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 * 1/2 = 1/6 = 0.16666666666666666. 

Example 2:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
Output: 0.3333333333333333
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after second 1. 

Example 3:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 20, target = 6
Output: 0.16666666666666666

Constraints:

Given an undirected tree consisting of n vertices numbered from 1 to n. A frog starts jumping from vertex 1. In one second, the frog jumps from its current vertex to another unvisited vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices, it jumps randomly to one of them with the same probability. Otherwise, when the frog can not jump to any unvisited vertex, it jumps forever on the same vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi.

Return the probability that after t seconds the frog is on the vertex target.

Example 1:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
Output: 0.16666666666666666 
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after second 1 and then jumping with 1/2 probability to vertex 4 after second 2. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 * 1/2 = 1/6 = 0.16666666666666666. 

Example 2:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
Output: 0.3333333333333333
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after second 1. 

Example 3:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 20, target = 6
Output: 0.16666666666666666

Constraints:

• 1 <= n <= 100
• edges.length == n - 1
• edges[i].length == 2
• 1 <= ai, bi <= n
• 1 <= t <= 50
• 1 <= target <= n
• Answers within 10-5 of the actual value will be accepted as correct.

Solution

class Solution {
public:
  double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {
    vector<vector<int>> neighbors(n + 1);
    vector<bool> vis(n + 1);
    vector<double> probability(n + 1);
    for(auto &edge : edges) {
      neighbors[edge[0]].push_back(edge[1]);
      neighbors[edge[1]].push_back(edge[0]);
    }
    neighbors[1].push_back(1);
    queue<int> q;

    q.push(1);
    probability[1] = 1;
    for(int i = 0; i < t && q.size(); ++i) {
      int sz = q.size();
      for(int node = 0; node < sz; ++node) {
        int pos = q.front();
        q.pop();
        vis[pos] = true;
        if(neighbors[pos].size() == 1) {
          continue;
        }
        double prob = probability[pos] / (neighbors[pos].size() - 1);
        for(auto child : neighbors[pos]) {
          if(vis[child]) continue;
          q.push(child);
          probability[child] = prob;
        }
        probability[pos] = 0;
      }
    }

    return probability[target];
  }
};

July LeetCoding Challenge 7

Description

Kth Smallest Element in a Sorted Matrix

Given an n x n matrix where each of the rows and columns are sorted in ascending order, return the kth smallest element in the matrix.

Note that it is the kth smallest element in the sorted order, not the kth distinct element.

Example 1:

Input: matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
Output: 13
Explanation: The elements in the matrix are [1,5,9,10,11,12,13,13,15], and the 8th smallest number is 13

Example 2:

Input: matrix = [[-5]], k = 1
Output: -5

Constraints:

• n == matrix.length
• n == matrix[i].length
• 1 <= n <= 300
• -109 <= matrix[i][j] <= 109
• All the rows and columns of matrix are guaranteed to be sorted in non-decreasing order.
• 1 <= k <= n2

Solution

class Solution {
public:
  int kthSmallest(vector<vector<int>>& matrix, int k) {
    int n = matrix.size();
    if(k == 1) return matrix.front().front();
    if(k == n * n) return matrix.back().back();
    priority_queue<int> pq;
    for(auto &row : matrix) {
      for(auto i : row) {
        pq.push(i);
        while(pq.size() > k) pq.pop();
      }
    }
    return pq.top();
  }
};

// Accepted
// 85/85 cases passed (36 ms)
// Your runtime beats 54.31 % of cpp submissions
// Your memory usage beats 33.33 % of cpp submissions (14.3 MB)

int num[90000];
class Solution {
public:
  int kthSmallest(vector<vector<int>>& matrix, int k) {
    if(k == 1) return matrix.front().front();
    int n = matrix.size();
    if(k == n * n) return matrix.back().back();
    memset(num, 0, sizeof(int) * n * n);
    int cnt = 0;
    for(auto &row : matrix) {
      for(auto i : row) {
        num[cnt++] = i;
      }
    }
    nth_element(num, num + k - 1, num + n * n);
    return num[k - 1];
  }
};

// Accepted
// 85/85 cases passed (24 ms)
// Your runtime beats 95.29 % of cpp submissions
// Your memory usage beats 57.08 % of cpp submissions (13.2 MB)

class Solution {
  int n;
  int count(vector<vector<int>>& matrix, int num) {
    int row = 0;
    int col = n - 1;
    int cnt = 0;
    while(row < n && col >= 0) {
      if(matrix[row][col] <= num) {
        cnt += col + 1;
        row += 1;
      } else {
        col -= 1;
      }
    }
    return cnt;
  }
public:
  int kthSmallest(vector<vector<int>>& matrix, int k) {
    n = matrix.size();
    int low = matrix.front().front();
    int high = matrix.back().back();
    if(k == 1) return low;
    if(k == n * n) return high;
    while(low < high) {
      int mid = (low + high) >> 1;
      if(count(matrix, mid) < k) {
        low = mid + 1;
      }else{
        high = mid;
      }
    }
    return low;
  }
};

// Accepted
// 85/85 cases passed (20 ms)
// Your runtime beats 99.01 % of cpp submissions
// Your memory usage beats 90.44 % of cpp submissions (13.1 MB)