Today is Saturday, I gonna review the tasks I've done this week, and finish today's leetcode's July LeetCoding Challenge with cpp.

LeetCode Review

Number of Ways to Stay in the Same Place After Some Steps

too easy to review

Construct the Lexicographically Largest Valid Sequence

too easy to review

Minimize Maximum Pair Sum in Array

too easy to review

Number of Dice Rolls With Target Sum

too easy to review

Capacity To Ship Packages Within D Days

too easy to review

Find K Closest Elements

using customized sorting

class Solution {
public:
  vector<int> findClosestElements(vector<int>& arr, int k, int x) {
    sort(arr.begin(), arr.end(), [=](int a, int b) {
      int da = abs(a - x);
      int db = abs(b - x);
      return da < db || (da == db && a < b);
    });
    vector<int> answer(arr.begin(), arr.begin() + k);
    sort(answer.begin(), answer.end());
    return answer;
  }
};

binary search for left boundary

class Solution {
public:
  vector<int> findClosestElements(vector<int>& arr, int k, int x) {
    int left = 0;
    int right = arr.size() - k;
    while(left < right) {
      int mid = (left + right) >> 1;
      if(x - arr[mid] > arr[mid + k] - x) {
        left = mid + 1;
      } else {
        right = mid;
      }
    }
    return vector<int>(arr.begin() + left, arr.begin() + left + k);
  }
};

Gray Code

too easy to review

Lowest Common Ancestor of a Binary Tree

too easy to review

Remove All Adjacent Duplicates In String

too easy to review

Max Consecutive Ones III

auto speedup = []() {
  std::ios::sync_with_stdio(false);
  cin.tie(nullptr);
  cout.tie(nullptr);
  return nullptr;
}();
class Solution {
public:
  int longestOnes(vector<int>& nums, int k) {
    int s = accumulate(nums.begin(), nums.end(), 0);
    int len = nums.size();
    if(s + k >= len) return len;
    int start = -1;
    int flip = 0;
    int answer = 0;
    for(int end = 0; end < len; ++end) {
      if(!nums[end]) {
        if(!k) {
          start = end;
        } else if(flip < k) {
          flip += 1;
        } else {
          start += 1;
          while(nums[start]) start += 1;
        }
      }
      answer = max(answer, end - start);
    }
    return answer;
  }
};

July LeetCoding Challenge 3

Description

Max Sum of Rectangle No Larger Than K

Given an m x n matrix matrix and an integer k, return the max sum of a rectangle in the matrix such that its sum is no larger than k.

It is guaranteed that there will be a rectangle with a sum no larger than k.

Example 1:

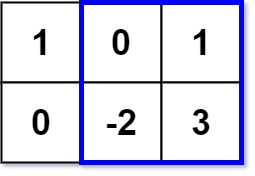
Input: matrix = [[1,0,1],[0,-2,3]], k = 2
Output: 2
Explanation: Because the sum of the blue rectangle [[0, 1], [-2, 3]] is 2, and 2 is the max number no larger than k (k = 2).

Example 2:

Input: matrix = [[2,2,-1]], k = 3
Output: 3

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -100 <= matrix[i][j] <= 100
• -105 <= k <= 105

Follow up: What if the number of rows is much larger than the number of columns?

Solution

class Solution {
public:
  int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
    int rows = matrix.size();
    int cols = matrix.front().size(); 
    // cout << "---------------" << endl;
    vector<vector<int>> prefix(rows, vector<int>(cols + 1));
    for(int i = 0; i < rows; ++i) {
      for(int j = 0; j < cols; ++j) {
        prefix[i][j + 1] = prefix[i][j] + matrix[i][j];
      }
    }

    int answer = INT_MIN;
    for(int i = 0; i < cols; ++i) {
      for(int j = i + 1; j <= cols; ++j) {
        set<int> tmp{0};
        int sum = 0;
        // cout << endl;
        for(int row = 0; row < rows; ++row) {
          sum += prefix[row][j] - prefix[row][i];
          // cout << i << ' ' << j << ' ' << row << ' ' << sum << endl;
          int diff = sum - k;
          auto it = tmp.lower_bound(diff);
          if(it != tmp.end()) {
            answer = max(answer, sum - *it);
            if(answer == k) return answer;
          }
          tmp.insert(sum);
        }
      }
    }

    return answer;
  }
};