Today I have done Binary Tree Maximum Path Sum and leetcode's June LeetCoding Challenge with cpp.

Binary Tree Maximum Path Sum

Description

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any path.

Example 1:

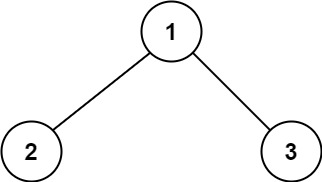
Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

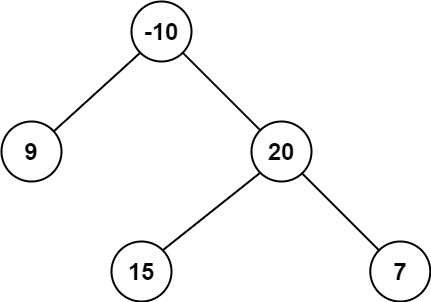
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Constraints:

• The number of nodes in the tree is in the range [1, 3 * 104].
• -1000 <= Node.val <= 1000

Solution

class Solution {
  int answer = INT_MIN;
  int solve(TreeNode* root) {
    if(!root) return 0;
    int maxLeft = solve(root->left);
    int maxRight = solve(root->right);
    int val = root->val;
    if(maxLeft > 0) val += maxLeft;
    if(maxRight > 0) val += maxRight;
    answer = max(answer, val);
    return (maxLeft < 0 && maxRight < 0) ? root->val :
           maxLeft > maxRight ? root->val + maxLeft :
                                root->val + maxRight;
  }
public:
  int maxPathSum(TreeNode* root) {
    solve(root);
    return answer;
  }
};

June LeetCoding Challenge 25

Description

Redundant Connection

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

Example 1:

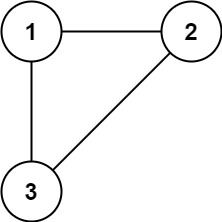
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

Example 2:

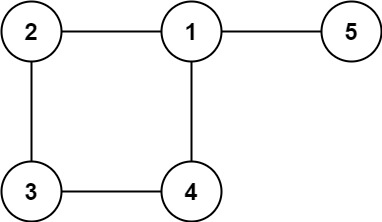
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

Constraints:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• There are no repeated edges.
• The given graph is connected.

Solution

class Solution {
  int parent[1000];

  int find(int x) {
    if(x != parent[x]) parent[x] = find(parent[x]);
    return parent[x];
  }
  
  void merge(int x, int y) {
    int px = find(x);
    int py = find(y);
    parent[px] = py;
  }

  void init() {
    for(int i = 0; i < 1000; i++) parent[i] = i;
  }
public:
  vector<int> findRedundantConnection(vector<vector<int>>& edges) {
    init();
    for(auto &edge : edges) {
      int x = edge[0] - 1;
      int y = edge[1] - 1;
      int px = find(x);
      int py = find(y);
      if(px != py) merge(x, y);
      else return edge;
    }
    return {-1, -1};
  }
};