Today I have done Cells with Odd Values in a Matrix and leetcode's June LeetCoding Challenge with cpp.

Cells with Odd Values in a Matrix

Description

There is an m x n matrix that is initialized to all 0's. There is also a 2D array indices where each indices[i] = [ri, ci] represents a 0-indexed location to perform some increment operations on the matrix.

For each location indices[i], do both of the following:

1. Increment all the cells on row ri.
2. Increment all the cells on column ci.

Given m, n, and indices, return the number of odd-valued cells in the matrix after applying the increment to all locations in indices.

Example 1:

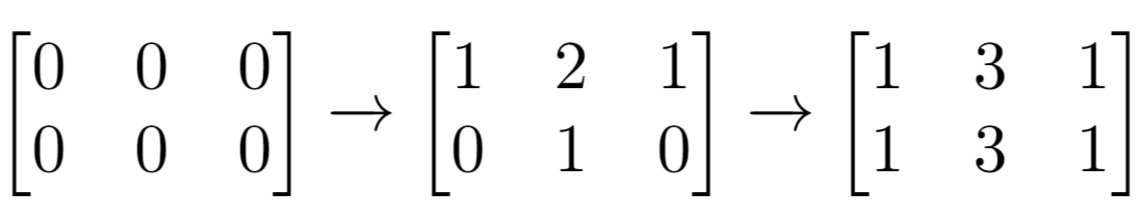
Input: m = 2, n = 3, indices = [[0,1],[1,1]]
Output: 6
Explanation: Initial matrix = [[0,0,0],[0,0,0]].
After applying first increment it becomes [[1,2,1],[0,1,0]].
The final matrix is [[1,3,1],[1,3,1]], which contains 6 odd numbers.

Example 2:

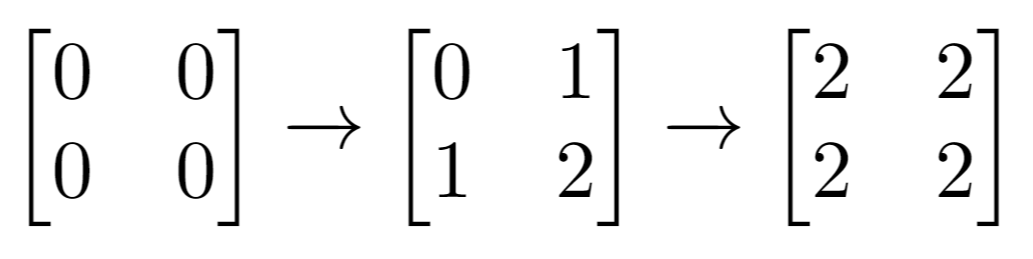
Input: m = 2, n = 2, indices = [[1,1],[0,0]]
Output: 0
Explanation: Final matrix = [[2,2],[2,2]]. There are no odd numbers in the final matrix.

Constraints:

• 1 <= m, n <= 50
• 1 <= indices.length <= 100
• 0 <= ri < m
• 0 <= ci < n

Follow up: Could you solve this in O(n + m + indices.length) time with only O(n + m) extra space?

Solution

class Solution {
public:
  int oddCells(int m, int n, vector<vector<int>>& indices) {
    bool bm[50] = {};
    bool bn[50] = {};
    for(auto &index : indices) {
      bm[index[0]] = !bm[index[0]];
      bn[index[1]] = !bn[index[1]];
    }
    int oddRows = 0;
    for(int i = 0; i < m; i++) oddRows += bm[i];
    int evenRows = m - oddRows;

    int answer = 0;
    for(int i = 0; i < n; i++) {
      if(bn[i]) answer += evenRows;
      else answer += oddRows;
    }
    return answer;
  }
};

June LeetCoding Challenge 17

Description

Number of Subarrays with Bounded Maximum

We are given an array nums of positive integers, and two positive integers left and right (left <= right).

Return the number of (contiguous, non-empty) subarrays such that the value of the maximum array element in that subarray is at least left and at most right.

Example:
Input: 
nums = [2, 1, 4, 3]
left = 2
right = 3
Output: 3
Explanation: There are three subarrays that meet the requirements: [2], [2, 1], [3].

Note:

• left, right, and nums[i] will be an integer in the range [0, 10^9].
• The length of nums will be in the range of [1, 50000].

Solution

auto speedup = [](){
  cin.tie(nullptr);
  cout.tie(nullptr);
  ios::sync_with_stdio(false);
  return 0;
}();
class Solution {
public:
  int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {
    int start = -1;
    int len = nums.size();
    int answer = 0;
    while(start < len) {
      while(start < len - 1 && nums[start + 1] > right) start += 1;
      int end = start + 1;
      int preStart = start;
      while(end < len && nums[end] <= right) end += 1;
      for(int i = start + 1; i < end; ++i) {
        if(nums[i] >= left && nums[i] <= right) {
          answer += (i - preStart) * (end - i);
          preStart = i;
        }
      }
      start = end;
    }
    return answer;
  }
};