Today I have done Valid Permutations for DI Sequence and leetcode's June LeetCoding Challenge with cpp.

Valid Permutations for DI Sequence

Description

We are given s, a length n string of characters from the set {'D', 'I'}. (These letters stand for "decreasing" and "increasing".)

A valid permutation is a permutation p[0], p[1], ..., p[n] of integers {0, 1, ..., n}, such that for all i:

• If s[i] == 'D', then p[i] > p[i+1], and;
• If s[i] == 'I', then p[i] < p[i+1].

How many valid permutations are there? Since the answer may be large, return your answer modulo 109 + 7.

Example 1:

Input: s = "DID"
Output: 5
Explanation: 
The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)

Note:

1. 1 <= s.length <= 200
2. s consists only of characters from the set {'D', 'I'}.

Solution

use $DP[i][j]$ representing amount of permutations that length is i + 1 and last element is j-th element of the rest. then, state transformation equations are:

$DP[i][j]=\left{\begin{matrix}1, i=0\0,i+j>len\\sum\limits_{j' = 0}^{j-1}dp[i-1][j'], S[i-1]\ is\ 'I'\\sum\limits_{j' =j}^{len}dp[i-1][j'], S[i-1]\ is\ 'D\end{matrix}\right.$

const int MOD = 1e9 + 7;
class Solution {
public:
  int numPermsDISequence(string s) {
    int dp[201][201] = {};
    int len = s.length();
    for(int i = 0; i <= len; ++i) dp[0][i] = 1;
    for(int i = 1; i <= len; ++i) {
      for(int j = 0; j + i <= len; ++j) {
        if(s[i - 1] == 'D') {
          dp[i][j] = 0;
          for(int k = len; k > j; --k) {
            dp[i][j] += dp[i - 1][k];
            dp[i][j] %= MOD;
          }
        } else {
          dp[i][j] = 0;
          for(int k = 0; k <= j; ++k) {
            dp[i][j] += dp[i - 1][k];
            dp[i][j] %= MOD;
          }
        }
      }
    }
    int answer = 0;
    for(int i = 0; i <= len; ++i) {
      answer += dp[len][i];
      answer %= MOD;
    }
    return answer;
  }
};

time complexity is $O(N^3)$, and we can use prefix sum to optimize the solution

const int MOD = 1e9 + 7;
class Solution {
public:
  int numPermsDISequence(string s) {
    int dp[201][201] = {};
    int len = s.length();
    for(int i = 0; i <= len; ++i) dp[0][i] = 1 + i;
    for(int i = 1; i <= len; ++i) {
      for(int j = 0; j <= len; ++j) {
        if(j + i > len) {
          dp[i][j] = dp[i][j - 1];
        } else if(s[i - 1] == 'D') {
          dp[i][j] = dp[i - 1][len] - dp[i - 1][j] + MOD;
          dp[i][j] %= MOD;
        } else {
          dp[i][j] = dp[i - 1][j];
        }
        if(j + i <= len && j) {
          dp[i][j] += j ? dp[i][j - 1] : 0;
          dp[i][j] %= MOD;
        }
        // cout << i << ' ' << j << ' ' << dp[i][j] << endl;
      }
    }
    return dp[len][len];
  }
};

thus, time complexity and space complexity are both $O(N^2)$

June LeetCoding Challenge 3

Description

Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts

Given a rectangular cake with height h and width w, and two arrays of integers horizontalCuts and verticalCuts where horizontalCuts[i] is the distance from the top of the rectangular cake to the ith horizontal cut and similarly, verticalCuts[j] is the distance from the left of the rectangular cake to the jth vertical cut.

Return the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays horizontalCuts and verticalCuts. Since the answer can be a huge number, return this modulo 10^9 + 7.

Example 1:

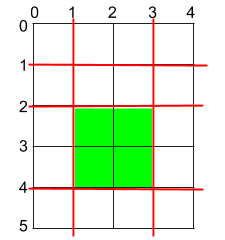
Input: h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
Output: 4 
Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.

Example 2:

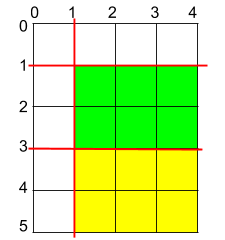
Input: h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
Output: 6
Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.

Example 3:

Input: h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
Output: 9

Constraints:

• 2 <= h, w <= 10^9
• 1 <= horizontalCuts.length < min(h, 10^5)
• 1 <= verticalCuts.length < min(w, 10^5)
• 1 <= horizontalCuts[i] < h
• 1 <= verticalCuts[i] < w
• It is guaranteed that all elements in horizontalCuts are distinct.
• It is guaranteed that all elements in verticalCuts are distinct.

Solution

const int MOD = 1e9 + 7;
class Solution {
public:
  int maxArea(int h, int w, vector<int>& horizontalCuts, vector<int>& verticalCuts) {
    int maxH = 0;
    int maxW = 0;
    int curH = 0;
    int curW = 0;
    sort(horizontalCuts.begin(), horizontalCuts.end());
    sort(verticalCuts.begin(), verticalCuts.end());
    for(auto h : horizontalCuts) {
      maxH = max(maxH, h - curH);
      curH = h;
    }
    maxH = max(maxH, h - curH);
    for(auto w : verticalCuts) {
      maxW = max(maxW, w - curW);
      curW = w;
    }
    maxW = max(maxW, w - curW);
    return 1LL * maxH * maxW % MOD;
  }
};