Today I have done Minimum Difficulty of a Job Schedule and leetcode's May LeetCoding Challenge with cpp.

Minimum Difficulty of a Job Schedule

Description

You want to schedule a list of jobs in d days. Jobs are dependent (i.e To work on the i-th job, you have to finish all the jobs j where 0 <= j < i).

You have to finish at least one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the d days. The difficulty of a day is the maximum difficulty of a job done in that day.

Given an array of integers jobDifficulty and an integer d. The difficulty of the i-th job is jobDifficulty[i].

Return the minimum difficulty of a job schedule. If you cannot find a schedule for the jobs return -1.

Example 1:

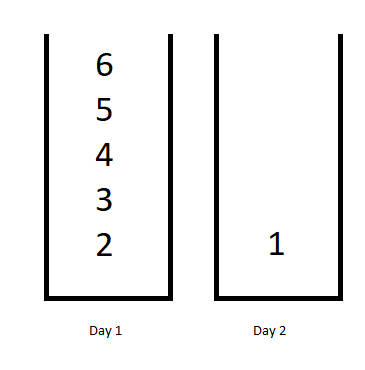
Input: jobDifficulty = [6,5,4,3,2,1], d = 2
Output: 7
Explanation: First day you can finish the first 5 jobs, total difficulty = 6.
Second day you can finish the last job, total difficulty = 1.
The difficulty of the schedule = 6 + 1 = 7 

Example 2:

Input: jobDifficulty = [9,9,9], d = 4
Output: -1
Explanation: If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.

Example 3:

Input: jobDifficulty = [1,1,1], d = 3
Output: 3
Explanation: The schedule is one job per day. total difficulty will be 3.

Example 4:

Input: jobDifficulty = [7,1,7,1,7,1], d = 3
Output: 15

Example 5:

Input: jobDifficulty = [11,111,22,222,33,333,44,444], d = 6
Output: 843

Constraints:

• 1 <= jobDifficulty.length <= 300
• 0 <= jobDifficulty[i] <= 1000
• 1 <= d <= 10

Solution

dp, using $dp[i][j]$ represents minimum value by completej jobs with i + 1 days

when $i = 0$, it's obvious that $dp[i][j] = max(jobDifficulty[0], jobDifficulty[1], ... ,jobDifficulty[j])$.

when $i > 0$, we first assign $dp[i][j]$ with $dp[i-1][j-1]+jobDifficulty[j]$, then we check if there are some jobs which have less difficulty before meet job with greater difficulty. And we can use monotonic stack accelerate whole process.

class Solution {
public:
  int minDifficulty(vector<int>& jobDifficulty, int d) {
    int len = jobDifficulty.size();
    if(len < d) return -1;
    if(len == d) return accumulate(jobDifficulty.begin(), jobDifficulty.end(), 0);
    int dp[d][len];
    dp[0][0] = jobDifficulty[0];
    for(int i = 1; i < len; ++i) dp[0][i] = max(dp[0][i - 1], jobDifficulty[i]);
    for(int i = 1; i < d; ++i) {
      vector<int> monoStack;
      for(int j = i; j < len; ++j) {
        dp[i][j] = dp[i - 1][j - 1] + jobDifficulty[j];
        while(monoStack.size() && jobDifficulty[monoStack.back()] < jobDifficulty[j]) {
          dp[i][j] = min(dp[i][j], dp[i][monoStack.back()] - jobDifficulty[monoStack.back()] + jobDifficulty[j]);
          monoStack.pop_back();
        }
        if(monoStack.size()) {
          dp[i][j] = min(dp[i][j], dp[i][monoStack.back()]);
        }
        monoStack.push_back(j);
      }
    }
    return dp[d - 1][len - 1];
  }
};

and some optimization

class Solution {
public:
  int minDifficulty(vector<int>& jobDifficulty, int d) {
    int len = jobDifficulty.size();
    if(len < d) return -1;
    if(len == d) return accumulate(jobDifficulty.begin(), jobDifficulty.end(), 0);
    if(len == 1) return *max_element(jobDifficulty.begin(), jobDifficulty.end());
    int dp[2][len];
    dp[0][0] = jobDifficulty[0];
    for(int i = 1; i < len; ++i) dp[0][i] = max(dp[0][i - 1], jobDifficulty[i]);
    for(int i = 1; i < d; ++i) {
      int parity = i & 1;
      vector<int> monoStack;
      for(int j = i; j < len; ++j) {
        dp[parity][j] = dp[!parity][j - 1] + jobDifficulty[j];
        while(monoStack.size() && jobDifficulty[monoStack.back()] < jobDifficulty[j]) {
          dp[parity][j] = min(dp[parity][j], dp[parity][monoStack.back()] - jobDifficulty[monoStack.back()] + jobDifficulty[j]);
          monoStack.pop_back();
        }
        if(monoStack.size()) {
          dp[parity][j] = min(dp[parity][j], dp[parity][monoStack.back()]);
        }
        monoStack.push_back(j);
      }
    }
    return dp[!(d&1)][len - 1];
  }
};

// Runtime: 4 ms, faster than 99.00% of C++ online submissions for Minimum Difficulty of a Job Schedule.
// Memory Usage: 7.1 MB, less than 99.47% of C++ online submissions for Minimum Difficulty of a Job Schedule.

May LeetCoding Challenge 28

Description

Maximum Erasure Value

You are given an array of positive integers nums and want to erase a subarray containing unique elements. The score you get by erasing the subarray is equal to the sum of its elements.

Return the maximum score you can get by erasing exactly one subarray.

An array b is called to be a subarray of a if it forms a contiguous subsequence of a, that is, if it is equal to a[l],a[l+1],...,a[r] for some (l,r).

Example 1:

Input: nums = [4,2,4,5,6]
Output: 17
Explanation: The optimal subarray here is [2,4,5,6].

Example 2:

Input: nums = [5,2,1,2,5,2,1,2,5]
Output: 8
Explanation: The optimal subarray here is [5,2,1] or [1,2,5].

Constraints:

• 1 <= nums.length <= 10^5
• 1 <= nums[i] <= 10^4

Solution

class Solution {
public:
  int maximumUniqueSubarray(vector<int>& nums) {
    bool vis[10001] = {};
    int sum = 0;
    int start = 0;
    int len = nums.size();
    int answer = 0;
    for(int end = 0; end < len; ++end) {
      while(vis[nums[end]]) {
        vis[nums[start]] = false;
        sum -= nums[start];
        start += 1;
      }
      vis[nums[end]] = true;
      sum += nums[end];
      answer = max(sum, answer);
    }
    return answer;
  }
};