Today I have done Jump Game VI and leetcode's May LeetCoding Challenge with cpp.

Jump Game VI

Description

You are given a 0-indexed integer array nums and an integer k.

You are initially standing at index 0. In one move, you can jump at most k steps forward without going outside the boundaries of the array. That is, you can jump from index i to any index in the range [i + 1, min(n - 1, i + k)] inclusive.

You want to reach the last index of the array (index n - 1). Your score is the sum of all nums[j] for each index j you visited in the array.

Return the maximum score you can get.

Example 1:

Input: nums = [1,-1,-2,4,-7,3], k = 2
Output: 7
Explanation: You can choose your jumps forming the subsequence [1,-1,4,3] (underlined above). The sum is 7.

Example 2:

Input: nums = [10,-5,-2,4,0,3], k = 3
Output: 17
Explanation: You can choose your jumps forming the subsequence [10,4,3] (underlined above). The sum is 17.

Example 3:

Input: nums = [1,-5,-20,4,-1,3,-6,-3], k = 2
Output: 0

Constraints:

• 1 <= nums.length, k <= 10^5
• -10^4 <= nums[i] <= 10^4

Solution

monotonic queue

class Solution {
public:
  int maxResult(vector<int>& nums, int k) {
    deque<int> monoQueue{nums[0]};
    int len = nums.size();
    for(int i = 1; i < min(k, len); ++i) {
      nums[i] += monoQueue.front();
      while(monoQueue.size() && monoQueue.back() < nums[i]) monoQueue.pop_back();
      monoQueue.push_back(nums[i]);
    }
    for(int i = k; i < len; ++i) {
      nums[i] += monoQueue.front();
      while(monoQueue.size() && monoQueue.back() < nums[i]) monoQueue.pop_back();
      if(monoQueue.size() && monoQueue.front() == nums[i - k]) monoQueue.pop_front();
      monoQueue.push_back(nums[i]);
    }
    return nums.back();
  }
};

May LeetCoding Challenge 6

Description

Convert Sorted List to Binary Search Tree

Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example 1:

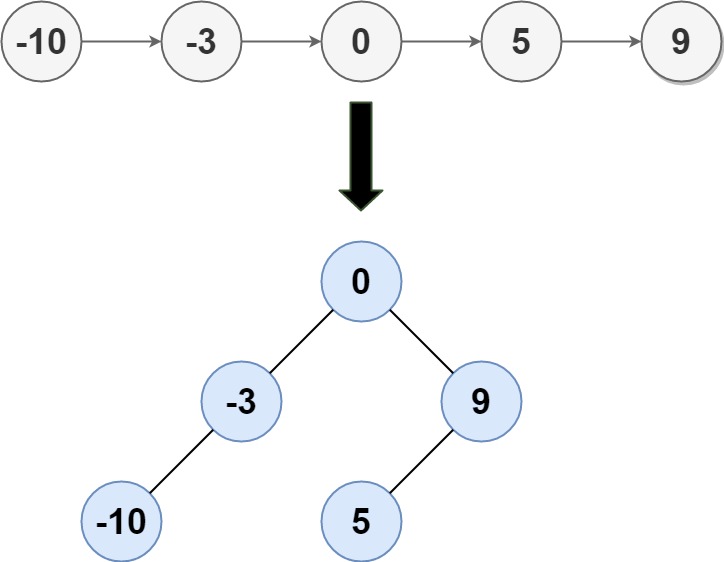
Input: head = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.

Example 2:

Input: head = []
Output: []

Example 3:

Input: head = [0]
Output: [0]

Example 4:

Input: head = [1,3]
Output: [3,1]

Constraints:

• The number of nodes in head is in the range [0, 2 * 10^4].
• -10^5 <= Node.val <= 10^5

Solution

done before

class Solution {
    ListNode *cur;
    
    int length(ListNode *head) {
        int len = 0;
        while(head) {
            len += 1;
            head = head->next;
        }
        return len;
    }
    
    TreeNode *buildBST(int begin, int end) {
        if(begin > end) return nullptr;
        
        int mid = (begin + end) >> 1;
        TreeNode *left = buildBST(begin, mid - 1);
        
        TreeNode *root = new TreeNode(cur->val);
        root->left = left;
        
        cur = cur->next;
        root->right = buildBST(mid + 1, end);
        
        return root;
    }
    
public:
    TreeNode* sortedListToBST(ListNode* head) {
        int len = length(head);
        cur = head;
        return buildBST(0, len-1);
    }
};