2021-04-17 Daily-Challenge
Today is Saturday, I gonna review the tasks I've done this week, and finish today's leetcode's April LeetCoding Challenge with cpp.
LeetCode Review
Beautiful Arrangement II
too easy to review
Flatten Nested List Iterator
already done a good work
Partition List
too easy to review
Fibonacci Number
already done a good work
Remove All Adjacent Duplicates in String II
too easy to review
Implement Trie (Prefix Tree)
too easy to review
Reverse Linked List
too easy to review
Average Salary Excluding the Minimum and Maximum Salary
too easy to review
LFU Cache
cpp got not LinkedHashSet, so I fail to implement a $O(1)$ solution this time.
class LFUCache {
int capacity;
unordered_map<int, int> kv;
unordered_map<int, int> cntKV;
unordered_map<int, int> freq;
unordered_map<int, set<pair<int, int>>> freqKey;
int min = INT_MAX;
int size = 0;
int cnt = 0;
public:
LFUCache(int c): capacity(c) { }
int get(int key) {
if(!kv.count(key)) return -1;
int f = freq[key];
freqKey[f].erase(make_pair(cntKV[key], key));
if(freqKey[f].empty()) {
freqKey.erase(f);
if(f == min) min = f + 1;
}
freqKey[f + 1].emplace(make_pair(++cnt, key));
cntKV[key] = cnt;
freq[key] = f + 1;
return kv[key];
}
void put(int key, int value) {
if(!capacity) return;
if(kv.count(key)) {
int f = freq[key];
freqKey[f].erase(make_pair(cntKV[key], key));
if(freqKey[f].empty()) {
freqKey.erase(f);
if(f == min) min = f + 1;
}
freqKey[f + 1].emplace(make_pair(++cnt, key));
freq[key] = f + 1;
} else {
if(size == capacity) {
size -= 1;
int removedKey = freqKey[min].begin()->second;
kv.erase(removedKey);
freqKey[min].erase(freqKey[min].begin());
if(freqKey[min].empty() && min != 1) freqKey.erase(min);
}
size += 1;
freqKey[1].emplace(make_pair(++cnt, key));
freq[key] = 1;
min = 1;
}
cntKV[key] = cnt;
kv[key] = value;
}
};
Find a Value of a Mysterious Function Closest to Target
I finally optimize it by quick return!
constexpr int maxBit(int x) {
for(int i = 30; i >= 0 ; --i){
if((1 << i) & x) return (1 << i);
}
return -1;
}
class Solution {
int len;
int closestToOneBit(vector<int>& arr, int bit, int target) {
int pos = 0;
int result = INT_MAX;
while(pos < len) {
if(!(arr[pos] & bit)) {
pos += 1;
} else {
int res = arr[pos];
while(pos < len && (arr[pos] & bit)) {
res &= arr[pos];
pos += 1;
}
result = min(result, abs(res - target));
}
}
return result;
}
public:
int closestToTarget(vector<int>& arr, int target) {
int all = (1 << 26) - 1;
len = arr.size();
int mmax = 0;
for(auto n : arr) {
mmax = max(n, mmax);
all &= n;
}
if(mmax <= target) return target - mmax;
if(all >= target) return all - target;
int mBit = (maxBit(target) << 1);
int bit = mBit;
int answer = INT_MAX;
while(bit) {
answer = min(answer, closestToOneBit(arr, bit, target));
if(answer != INT_MAX && (mBit >> 2) > bit) return answer;
bit >>= 1;
}
return answer;
}
};
// Runtime: 88 ms, faster than 95.69% of C++ online submissions for Find a Value of a Mysterious Function Closest to Target.
// Memory Usage: 62.5 MB, less than 88.79% of C++ online submissions for Find a Value of a Mysterious Function Closest to Target.
April LeetCoding Challenge 17
Description
Number of Submatrices That Sum to Target
Given a matrix and a target, return the number of non-empty submatrices that sum to target.
A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.
Two submatrices (x1, y1, x2, y2) and (x1', y1', x2', y2') are different if they have some coordinate that is different: for example, if x1 != x1'.
Example 1:
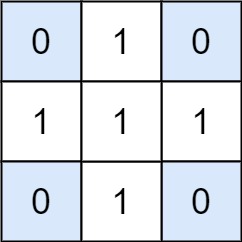
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.
Example 2:
Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.
Example 3:
Input: matrix = [[904]], target = 0
Output: 0
Constraints:
1 <= matrix.length <= 1001 <= matrix[0].length <= 100-1000 <= matrix[i] <= 1000-10^8 <= target <= 10^8
Solution
class Solution {
public:
int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
int rows = matrix.size();
int cols = matrix.front().size();
vector<vector<int>> sum(rows + 1, vector<int>(cols + 1));
for(int i = 0; i < rows; ++i) {
for(int j = 0; j < cols; ++j) {
sum[i + 1][j + 1] = sum[i + 1][j] + sum[i][j + 1] - sum[i][j] + matrix[i][j];
}
}
int answer = 0;
for(int i = 0; i < cols; ++i) {
for(int j = i + 1; j <= cols; ++j) {
multiset<int> tmp{0};
for(int row = 1; row <= rows; ++row) {
int curSum = sum[row][j] - sum[row][i];
answer += tmp.count(curSum - target);
tmp.insert(curSum);
}
}
}
return answer;
}
};
// 40 / 40 test cases passed.
// Status: Accepted
// Runtime: 572 ms
// Memory Usage: 166 MB
using map is slower, maybe due to insertion and initialization?
class Solution {
public:
int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
int rows = matrix.size();
int cols = matrix.front().size();
vector<vector<int>> sum(rows + 1, vector<int>(cols + 1));
for(int i = 0; i < rows; ++i) {
for(int j = 0; j < cols; ++j) {
sum[i + 1][j + 1] = sum[i + 1][j] + sum[i][j + 1] - sum[i][j] + matrix[i][j];
}
}
int answer = 0;
for(int i = 0; i < cols; ++i) {
for(int j = i + 1; j <= cols; ++j) {
map<int, int> tmp{{0, 1}};
for(int row = 1; row <= rows; ++row) {
int curSum = sum[row][j] - sum[row][i];
answer += tmp[curSum - target];
tmp[curSum] += 1;
}
}
}
return answer;
}
};
// 40 / 40 test cases passed.
// Status: Accepted
// Runtime: 972 ms
// Memory Usage: 274.8 MB
yes
class Solution {
public:
int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
int rows = matrix.size();
int cols = matrix.front().size();
vector<vector<int>> sum(rows + 1, vector<int>(cols + 1));
for(int i = 0; i < rows; ++i) {
for(int j = 0; j < cols; ++j) {
sum[i + 1][j + 1] = sum[i + 1][j] + sum[i][j + 1] - sum[i][j] + matrix[i][j];
}
}
int answer = 0;
for(int i = 0; i < cols; ++i) {
for(int j = i + 1; j <= cols; ++j) {
map<int, int> tmp{{0, 1}};
for(int row = 1; row <= rows; ++row) {
int curSum = sum[row][j] - sum[row][i];
answer += tmp.count(curSum - target) ? tmp[curSum - target] : 0;
tmp[curSum] += 1;
}
}
}
return answer;
}
};
// 40 / 40 test cases passed.
// Status: Accepted
// Runtime: 648 ms
// Memory Usage: 164.9 MB
unordered_set is similar
class Solution {
public:
int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
int rows = matrix.size();
int cols = matrix.front().size();
vector<vector<int>> sum(rows + 1, vector<int>(cols + 1));
for(int i = 0; i < rows; ++i) {
for(int j = 0; j < cols; ++j) {
sum[i + 1][j + 1] = sum[i + 1][j] + sum[i][j + 1] - sum[i][j] + matrix[i][j];
}
}
int answer = 0;
for(int i = 0; i < cols; ++i) {
for(int j = i + 1; j <= cols; ++j) {
unordered_map<int, int> tmp{{0, 1}};
for(int row = 1; row <= rows; ++row) {
int curSum = sum[row][j] - sum[row][i];
answer += tmp.count(curSum - target) ? tmp[curSum - target] : 0;
tmp[curSum] += 1;
}
}
}
return answer;
}
};
// 40 / 40 test cases passed.
// Status: Accepted
// Runtime: 612 ms
// Memory Usage: 174 MB
optimization with principle of locality seems useless
class Solution {
public:
int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
int rows = matrix.size();
int cols = matrix.front().size();
vector<vector<int>> rowPrefix(rows, vector<int>(cols + 1));
for(int i = 0; i < rows; ++i) {
for(int j = 0; j < cols; ++j) {
rowPrefix[i][j + 1] = rowPrefix[i][j] + matrix[i][j];
}
}
int answer = 0;
for(int i = 0; i < cols; ++i) {
for(int j = i + 1; j <= cols; ++j) {
int sum = 0;
multiset<int> tmp{0};
for(int row = 0; row < rows; ++row) {
sum += rowPrefix[row][j] - rowPrefix[row][i];
answer += tmp.count(sum - target);
tmp.insert(sum);
}
}
}
return answer;
}
};
// 40 / 40 test cases passed.
// Status: Accepted
// Runtime: 596 ms
// Memory Usage: 166 MB