Today I have done Minimum Moves to Move a Box to Their Target Location and leetcode's March LeetCoding Challenge with cpp.

Minimum Moves to Move a Box to Their Target Location

Description

Storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.

The game is represented by a grid of size m x n, where each element is a wall, floor, or a box.

Your task is move the box 'B' to the target position 'T' under the following rules:

• Player is represented by character 'S' and can move up, down, left, right in the grid if it is a floor (empy cell).
• Floor is represented by character '.' that means free cell to walk.
• Wall is represented by character '#' that means obstacle (impossible to walk there).
• There is only one box 'B' and one target cell 'T' in the grid.
• The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a push.
• The player cannot walk through the box.

Return the minimum number of pushes to move the box to the target. If there is no way to reach the target, return -1.

Example 1:

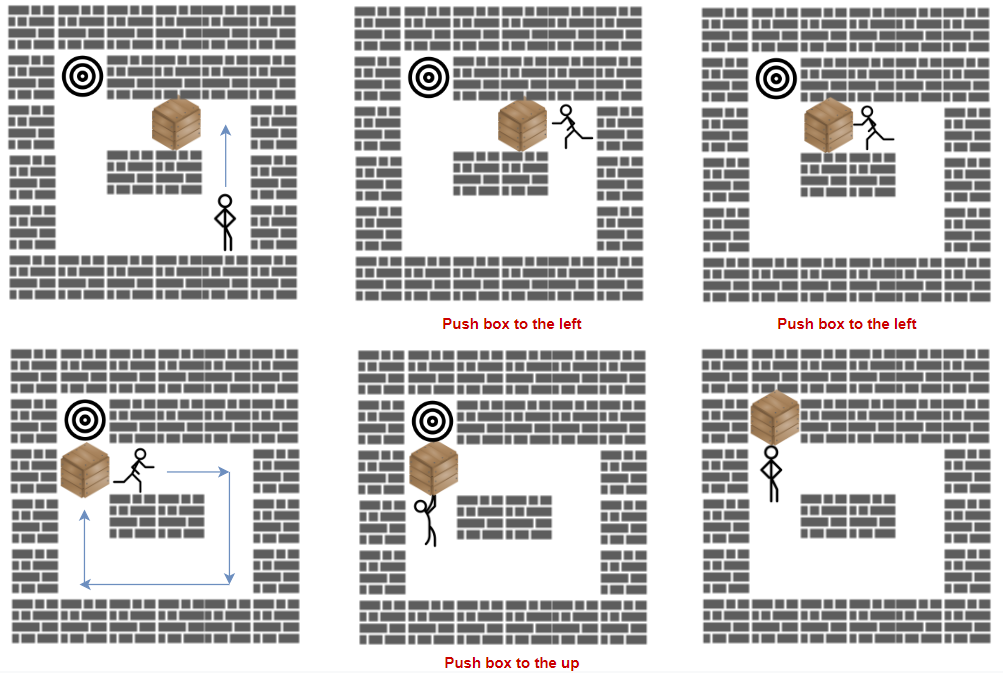
Input: grid = [["#","#","#","#","#","#"],
               ["#","T","#","#","#","#"],
               ["#",".",".","B",".","#"],
               ["#",".","#","#",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: 3
Explanation: We return only the number of times the box is pushed.

Example 2:

Input: grid = [["#","#","#","#","#","#"],
               ["#","T","#","#","#","#"],
               ["#",".",".","B",".","#"],
               ["#","#","#","#",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: -1

Example 3:

Input: grid = [["#","#","#","#","#","#"],
               ["#","T",".",".","#","#"],
               ["#",".","#","B",".","#"],
               ["#",".",".",".",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: 5
Explanation:  push the box down, left, left, up and up.

Example 4:

Input: grid = [["#","#","#","#","#","#","#"],
               ["#","S","#",".","B","T","#"],
               ["#","#","#","#","#","#","#"]]
Output: -1

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m <= 20
• 1 <= n <= 20
• grid contains only characters '.', '#', 'S' , 'T', or 'B'.
• There is only one character 'S', 'B' and 'T' in the grid.

Solution

simulation and BFS.

because we only care about times we push, so we don't need to care about how we step to the position to push the box.

every time we search for valid pushes, then apply it and check if it's a state we already done before.

I'm surprised that passed it at the first time.

class Solution {
    int cols;
    int rows;
    void print(string &cur) {
        // only for debug
        // but 1AC!
        cout << "$$$$$$$$$$$$$$$$" << endl;
        for(int i = 0; i < rows; ++i) {
            cout << cur.substr(i*cols, cols) << endl;
        }
        cout << "$$$$$$$$$$$$$$$$" << endl;
    }
    bool isEnd(string &state) {
        for(auto c : state) if(c == 'T') return false;
        return true;
    }
    string gridToString(vector<vector<char>> &grid) {
        string res;
        for(auto &v : grid) {
            for(auto c : v) {
                res.push_back(c);
            }
        }
        return res;
    }
    
    vector<int> checkValidPush(string curState) {
        vector<int> moves = {1, -1, cols, -cols};
        int bPos = -1, sPos = -1;
        for(int i = 0; i < curState.length(); ++i) {
            if(curState[i] == 'B') {
                bPos = i;
            }
            if(curState[i] == 'S') {
                sPos = i;
            }
        }
        vector<int> validMove;
        queue<int> q;
        q.push(sPos);
        while(!q.empty()) {
            int cur = q.front();
            q.pop();
            for(auto move : moves) {
                int next = cur + move;
                if(next >= curState.length() || next < 0 || 
                   (next % cols == 0 && move == 1) ||
                   (next % cols == cols - 1 && move == -1)
                  || (curState[next] != '.' && curState[next] != 'T')) {
                    continue;
                }
                curState[next] = 'S';
                q.push(next);
            }
        }
        // print(curState);
        for(auto move : moves) {
            int player = bPos - move;
            int next = bPos + move;
            if(player < 0 || player >= curState.length() || curState[player] != 'S') continue;
            if(next < 0 || next >= curState.length() || curState[next] == '#') continue;
            validMove.push_back(move);
        }
        return move(validMove);
    }
    
    string applyPush(int push, string curState) {
        int bPos = -1, sPos = -1;
        for(int i = 0; i < curState.length(); ++i) {
            if(curState[i] == 'B') {
                bPos = i;
            }
            if(curState[i] == 'S') {
                sPos = i;
            }
        }
        curState[sPos] = '.';
        curState[bPos] = 'S';
        curState[bPos + push] = 'B';
        return curState;
    }
public:
    int minPushBox(vector<vector<char>>& grid) {
        rows = grid.size();
        cols = grid.front().size();
        string beginState = gridToString(grid);
        unordered_map<string, int> moves;
        moves[beginState] = 0;
        queue<string> q;
        q.push(beginState);
        while(!q.empty()) {
            string cur = q.front();
            q.pop();
            if(isEnd(cur)) return moves[cur];
            auto pushes = checkValidPush(cur);
            for(auto push: pushes) {
                auto res = applyPush(push, cur);
                if(!moves.count(res)) {
                    moves[res] = moves[cur] + 1;
                    q.push(res);
                }
            }
        }
        return -1;
    }
};

March LeetCoding Challenge 9

Description

Remove Palindromic Subsequences

Given the root of a binary tree, then value v and depth d, you need to add a row of nodes with value v at the given depth d. The root node is at depth 1.

The adding rule is: given a positive integer depth d, for each NOT null tree nodes N in depth d-1, create two tree nodes with value v as N's left subtree root and right subtree root. And N's original left subtree should be the left subtree of the new left subtree root, its original right subtree should be the right subtree of the new right subtree root. If depth d is 1 that means there is no depth d-1 at all, then create a tree node with value v as the new root of the whole original tree, and the original tree is the new root's left subtree.

Example 1:

Input: 
A binary tree as following:
       4
     /   \
    2     6
   / \   / 
  3   1 5   

v = 1

d = 2

Output: 
       4
      / \
     1   1
    /     \
   2       6
  / \     / 
 3   1   5   

Example 2:

Input: 
A binary tree as following:
      4
     /   
    2    
   / \   
  3   1    

v = 1

d = 3

Output: 
      4
     /   
    2
   / \    
  1   1
 /     \  
3       1

Note:

1. The given d is in range [1, maximum depth of the given tree + 1].
2. The given binary tree has at least one tree node.

Solution

ah ha, only one function~

class Solution {
public:
    TreeNode* addOneRow(TreeNode* root, int v, int d, bool left = true) {
        if(d == 1) {
            TreeNode *newRoot = new TreeNode(v);
            if(left) newRoot->left = root;
            else newRoot->right = root;
            return newRoot;
        }
        if(!root) return nullptr;
        root->left = addOneRow(root->left, v, d-1, true);
        root->right = addOneRow(root->right, v, d-1, false);
        return root;
    }
};