Today I have done Bulb Switcher III and leetcode's February LeetCoding Challenge with cpp.

Bulb Switcher III

Description

There is a room with n bulbs, numbered from 1 to n, arranged in a row from left to right. Initially, all the bulbs are turned off.

At moment k (for k from 0 to n - 1), we turn on the light[k] bulb. A bulb change color to blue only if it is on and all the previous bulbs (to the left) are turned on too.

Return the number of moments in which all turned on bulbs are blue.

Example 1:

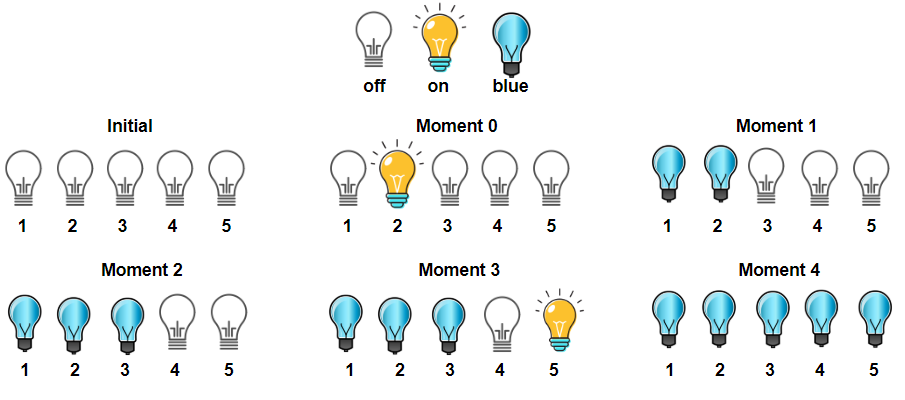
Input: light = [2,1,3,5,4]
Output: 3
Explanation: All bulbs turned on, are blue at the moment 1, 2 and 4.

Example 2:

Input: light = [3,2,4,1,5]
Output: 2
Explanation: All bulbs turned on, are blue at the moment 3, and 4 (index-0).

Example 3:

Input: light = [4,1,2,3]
Output: 1
Explanation: All bulbs turned on, are blue at the moment 3 (index-0).
Bulb 4th changes to blue at the moment 3.

Example 4:

Input: light = [2,1,4,3,6,5]
Output: 3

Example 5:

Input: light = [1,2,3,4,5,6]
Output: 6

Constraints:

• n == light.length
• 1 <= n <= 5 * 10^4
• light is a permutation of [1, 2, ..., n]

Solution

class Solution {
public:
    int numTimesAllBlue(vector<int>& light) {
        int cnt = 0;
        int right = 0;
        int answer = 0;
        for(auto i : light) {
            right = max(right, i);
            cnt += 1;
            answer += (cnt == right);
        }
        return answer;
    }
};

February LeetCoding Challenge 23

Description

Search a 2D Matrix II

Write an efficient algorithm that searches for a target value in an m x n integer matrix. The matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

Example 1:

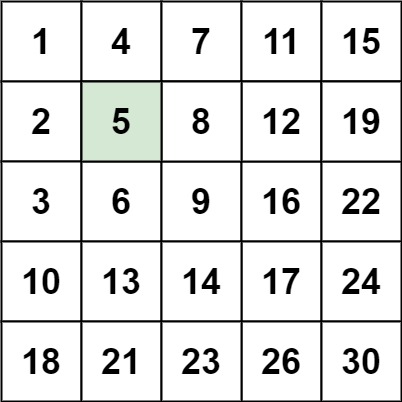
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
Output: true

Example 2:

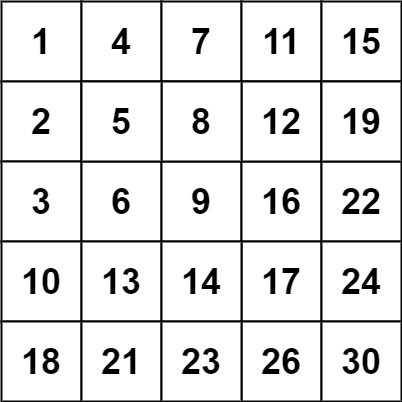
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
Output: false

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• $-10^9 \le matix[i][j] \le 10^9$
• All the integers in each row are sorted in ascending order.
• All the integers in each column are sorted in ascending order.
• $-10^9 \le target \le 10^9$

Solution

bad binary search, doubt if it's slower than binary search

class Solution {
    bool searchInMatrix(vector<vector<int>>& matrix, int target, int top, int down, int left, int right) {
        if(top > down || left > right) return false;
        int verticalMiddle = (top + down) >> 1;
        int horizontalMiddle = (left + right) >> 1;
        if(matrix[verticalMiddle][horizontalMiddle] == target) return true;
        if(matrix[verticalMiddle][horizontalMiddle] > target) {
            return searchInMatrix(matrix, target, top, verticalMiddle-1, horizontalMiddle, right) ||
                   searchInMatrix(matrix, target, verticalMiddle, down, left, horizontalMiddle-1) ||
                   searchInMatrix(matrix, target, top, verticalMiddle-1, left, horizontalMiddle-1);
        } else {
            return searchInMatrix(matrix, target, top, verticalMiddle, horizontalMiddle+1, right) ||
                   searchInMatrix(matrix, target, verticalMiddle+1, down, left, horizontalMiddle) ||
                   searchInMatrix(matrix, target, verticalMiddle+1, down, horizontalMiddle+1, right);
        }
    }
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size();
        int n = matrix.front().size();
        return searchInMatrix(matrix, target, 0, m-1, 0, n-1);
    }
};

// 128 / 128 test cases passed.
// Status: Accepted
// Runtime: 1884 ms
// Memory Usage: 14.8 MB

oh shit

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        for(auto &row : matrix) for(auto num : row) if(num == target) return true;
        return false;
    }
};

// 128 / 128 test cases passed.
// Status: Accepted
// Runtime: 604 ms
// Memory Usage: 14.9 MB