Today I have done Count All Possible Route and leetcode's February LeetCoding Challenge with cpp.

Count All Possible Routes

Description

You are given an array of distinct positive integers locations where locations[i] represents the position of city i. You are also given integers start, finish and fuel representing the starting city, ending city, and the initial amount of fuel you have, respectively.

At each step, if you are at city i, you can pick any city j such that j != i and 0 <= j < locations.length and move to city j. Moving from city i to city j reduces the amount of fuel you have by |locations[i] - locations[j]|. Please notice that |x| denotes the absolute value of x.

Notice that fuel cannot become negative at any point in time, and that you are allowed to visit any city more than once (including start and finish).

Return the count of all possible routes from start to finish.

Since the answer may be too large, return it modulo 10^9 + 7.

Example 1:

Input: locations = [2,3,6,8,4], start = 1, finish = 3, fuel = 5
Output: 4
Explanation: The following are all possible routes, each uses 5 units of fuel:
1 -> 3
1 -> 2 -> 3
1 -> 4 -> 3
1 -> 4 -> 2 -> 3

Example 2:

Input: locations = [4,3,1], start = 1, finish = 0, fuel = 6
Output: 5
Explanation: The following are all possible routes:
1 -> 0, used fuel = 1
1 -> 2 -> 0, used fuel = 5
1 -> 2 -> 1 -> 0, used fuel = 5
1 -> 0 -> 1 -> 0, used fuel = 3
1 -> 0 -> 1 -> 0 -> 1 -> 0, used fuel = 5

Example 3:

Input: locations = [5,2,1], start = 0, finish = 2, fuel = 3
Output: 0
Explanation: It's impossible to get from 0 to 2 using only 3 units of fuel since the shortest route needs 4 units of fuel.

Example 4:

Input: locations = [2,1,5], start = 0, finish = 0, fuel = 3
Output: 2
Explanation: There are two possible routes, 0 and 0 -> 1 -> 0.

Example 5:

Input: locations = [1,2,3], start = 0, finish = 2, fuel = 40
Output: 615088286
Explanation: The total number of possible routes is 2615088300. Taking this number modulo 10^9 + 7 gives us 615088286.

Constraints:

• 2 <= locations.length <= 100
• 1 <= locations[i] <= 10^9
• All integers in locations are distinct.
• 0 <= start, finish < locations.length
• 1 <= fuel <= 200

Solution

simple dp

class Solution {
    const int MOD = 1e9 + 7;
public:
    int countRoutes(vector<int>& locations, int start, int finish, int fuel) {
        int cityLen = locations.size();
        vector<vector<int>> dp(cityLen, vector<int>(fuel + 1));
        vector<vector<bool>> vis(cityLen, vector<bool>(fuel + 1));
        dp[start][0] = 1;
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
        for(int i = 0; i < cityLen; ++i) {
            if(i == start) continue;
            int cost = abs(locations[start] - locations[i]);
            if(cost <= fuel) {
                q.push(make_pair(cost, i));
                dp[i][cost] = 1;
                vis[i][cost] = true;
            }
        }
        
        while(!q.empty()) {
            auto [cost, pos] = q.top();
            q.pop();
            if(cost > fuel) break;
            for(int i = 0; i < cityLen; ++i) {
                if(i == pos) continue;
                int newCost = abs(locations[pos] - locations[i]) + cost;
                if(newCost <= fuel) {
                    dp[i][newCost] = (dp[i][newCost] + dp[pos][cost]) % MOD;
                    if(!vis[i][newCost]) {
                        q.push(make_pair(newCost, i));
                        vis[i][newCost] = true;
                    }
                }
            }
        }
        int answer = 0;
        for(auto i : dp[finish]) {
            answer = (answer + i) % MOD;
        }
        return answer;
    }
};

February LeetCoding Challenge 2

Description

Trim a Binary Search Tree

Given the root of a binary search tree and the lowest and highest boundaries as low and high, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a unique answer.

Return the root of the trimmed binary search tree. Note that the root may change depending on the given bounds.

Example 1:

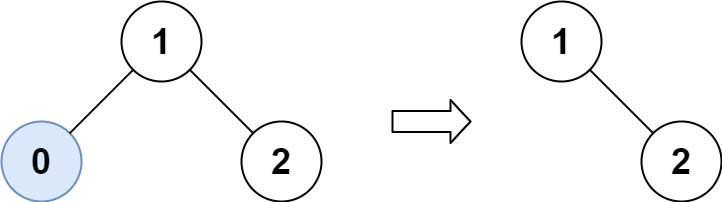
Input: root = [1,0,2], low = 1, high = 2
Output: [1,null,2]

Example 2:

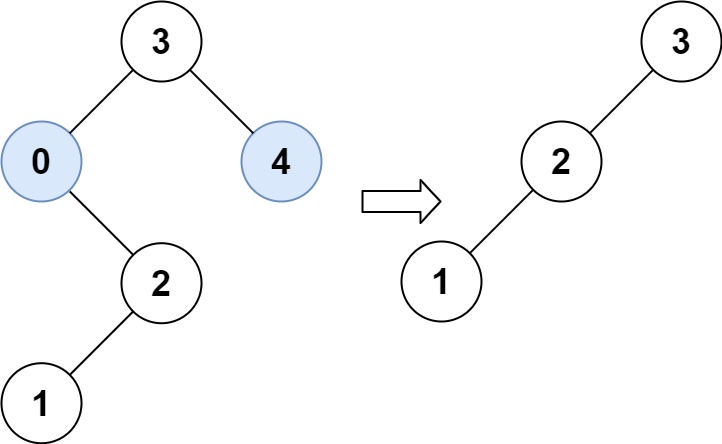
Input: root = [3,0,4,null,2,null,null,1], low = 1, high = 3
Output: [3,2,null,1]

Example 3:

Input: root = [1], low = 1, high = 2
Output: [1]

Example 4:

Input: root = [1,null,2], low = 1, high = 3
Output: [1,null,2]

Example 5:

Input: root = [1,null,2], low = 2, high = 4
Output: [2]

Constraints:

• The number of nodes in the tree in the range [1, 104].
• $0 \le Node.val \le 10^4$`
• The value of each node in the tree is unique.
• root is guaranteed to be a valid binary search tree.
• $0 \le low \le high\le 10^4$

Solution

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if(!root) return root;
        if(root->val < low) return trimBST(root->right, low, high);
        if(root->val > high) return trimBST(root->left, low, high);
        while(root->left && root->left->val < low) root->left = root->left->right;
        root->left = trimBST(root->left, low, high);
        while(root->right && root->right->val > high) root->right = root->right->left;
        root->right = trimBST(root->right, low, high);
        return root;
    }
};