Today I have done Largest Component Size by Common Factor, Implement Magic Dictionary, Possible Bipartition and leetcode's January LeetCoding Challenge with cpp.

Largest Component Size by Common Factor

Description

Given a non-empty array of unique positive integers A, consider the following graph:

• There are A.length nodes, labelled A[0] to A[A.length - 1];
• There is an edge between A[i] and A[j] if and only if A[i] and A[j] share a common factor greater than 1.

Return the size of the largest connected component in the graph.

Example 1:

Input: [4,6,15,35]
Output: 4

Example 2:

Input: [20,50,9,63]
Output: 2

Example 3:

Input: [2,3,6,7,4,12,21,39]
Output: 8

Note:

1. 1 <= A.length <= 20000
2. 1 <= A[i] <= 100000

Solution

I remembered union set but failed to AC it

class Solution {
    unordered_map<int, int> parent, count;

    int find(int x) {
        if(!parent.count(x)) parent[x] = x;
        else if(x != parent[x]) parent[x] = find(parent[x]);
        return parent[x];
    }

    void merge(int a, int b) {
        a = find(a);
        b = find(b);
        parent[a] = b;
    }
public:
    int largestComponentSize(vector<int>& A) {
        for(auto num : A) {
            for(int i = 2; i*i <= num; ++i) {
                if(num % i == 0) {
                    merge(num, i);
                    merge(num, num / i);
                }
            }
        }
        for(auto num : A) count[find(num)] += 1;
        int answer = 0;
        for(auto [_, cnt] : count) answer = max(answer, cnt);
        return answer;
    }
};

Possible Bipartition

Description

Design a data structure that is initialized with a list of different words. Provided a string, you should determine if you can change exactly one character in this string to match any word in the data structure.

Implement the MagicDictionary class:

• MagicDictionary() Initializes the object.
• void buildDict(String[] dictionary) Sets the data structure with an array of distinct strings dictionary.
• bool search(String searchWord) Returns true if you can change exactly one character in searchWord to match any string in the data structure, otherwise returns false.

Example 1:

Input
["MagicDictionary", "buildDict", "search", "search", "search", "search"]
[[], [["hello", "leetcode"]], ["hello"], ["hhllo"], ["hell"], ["leetcoded"]]
Output
[null, null, false, true, false, false]

Explanation
MagicDictionary magicDictionary = new MagicDictionary();
magicDictionary.buildDict(["hello", "leetcode"]);
magicDictionary.search("hello"); // return False
magicDictionary.search("hhllo"); // We can change the second 'h' to 'e' to match "hello" so we return True
magicDictionary.search("hell"); // return False
magicDictionary.search("leetcoded"); // return False

Constraints:

• 1 <= dictionary.length <= 100
• 1 <= dictionary[i].length <= 100
• dictionary[i] consists of only lower-case English letters.
• All the strings in dictionary are distinct.
• 1 <= searchWord.length <= 100
• searchWord consists of only lower-case English letters.
• buildDict will be called only once before search.
• At most 100 calls will be made to search.

Solution

class MagicDictionary {
    unordered_map<int, vector<string>> dict;
public:
    /** Initialize your data structure here. */
    MagicDictionary() {}
    
    void buildDict(vector<string> dictionary) {
        for(auto &s : dictionary) {
            dict[s.length()].push_back(s);
        }
    }
    
    bool search(string searchWord) {
        int len = searchWord.length();
        for(auto &s : dict[len]) {
            int count = 0;
            for(int i = 0; i < len; ++i) count += s[i] != searchWord[i];
            if(count == 1) return true;
        }
        return false;
    }
};

/**
 * Your MagicDictionary object will be instantiated and called as such:
 * MagicDictionary* obj = new MagicDictionary();
 * obj->buildDict(dictionary);
 * bool param_2 = obj->search(searchWord);
 */

Implement Magic Dictionary

Description

Given a set of N people (numbered 1, 2, ..., N), we would like to split everyone into two groups of any size.

Each person may dislike some other people, and they should not go into the same group.

Formally, if dislikes[i] = [a, b], it means it is not allowed to put the people numbered a and b into the same group.

Return true if and only if it is possible to split everyone into two groups in this way.

Example 1:

Input: N = 4, dislikes = [[1,2],[1,3],[2,4]]
Output: true
Explanation: group1 [1,4], group2 [2,3]

Example 2:

Input: N = 3, dislikes = [[1,2],[1,3],[2,3]]
Output: false

Example 3:

Input: N = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]]
Output: false

Constraints:

• 1 <= N <= 2000
• 0 <= dislikes.length <= 10000
• dislikes[i].length == 2
• 1 <= dislikes[i][j] <= N
• dislikes[i][0] < dislikes[i][1]
• There does not exist i != j for which dislikes[i] == dislikes[j].

Solution

DFS find bipartite graph

class Solution {
    vector<vector<int>> dislike;
    vector<int> group;
public:
    bool possibleBipartition(int N, vector<vector<int>>& dislikes) {
        dislike.resize(N+1);
        group.resize(N+1, -1);

        for(auto &dis : dislikes) {
            dislike[dis[0]].push_back(dis[1]);
            dislike[dis[1]].push_back(dis[0]);
        }

        int count = 0;
        while(count < N) {
            queue<int> q;
            for(int i = 1; i <= N; ++i) {
                if(group[i] == -1) {
                    q.push(i);
                    group[i] = 0;
                    break;
                }
            }

            count += 1;
            while(!q.empty()) {
                int current = q.front();
                q.pop();
                for(auto dis : dislike[current]) {
                    // cout << current << group[current] << dis << group[dis] << endl;
                    if(group[dis] != -1 && group[dis] != (group[current]^1)) return false;
                    if(group[dis] == -1) {
                        q.push(dis);
                        count += 1;
                    }
                    group[dis] = group[current]^1;
                }
            }
        }
        return count == N;
    }
};

January LeetCoding Challenge 29

Description

Vertical Order Traversal of a Binary Tree

Given the root of a binary tree, calculate the vertical order traversal of the binary tree.

For each node at position (x, y), its left and right children will be at positions (x - 1, y - 1) and (x + 1, y - 1) respectively.

The vertical order traversal of a binary tree is a list of non-empty reports for each unique x-coordinate from left to right. Each report is a list of all nodes at a given x-coordinate. The report should be primarily sorted by y-coordinate from highest y-coordinate to lowest. If any two nodes have the same y-coordinate in the report, the node with the smaller value should appear earlier.

Return the vertical order traversal of the binary tree.

Example 1:

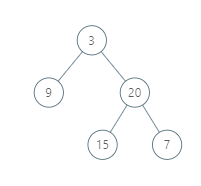
Input: root = [3,9,20,null,null,15,7]
Output: [[9],[3,15],[20],[7]]
Explanation: Without loss of generality, we can assume the root node is at position (0, 0):
The node with value 9 occurs at position (-1, -1).
The nodes with values 3 and 15 occur at positions (0, 0) and (0, -2).
The node with value 20 occurs at position (1, -1).
The node with value 7 occurs at position (2, -2).

Example 2:

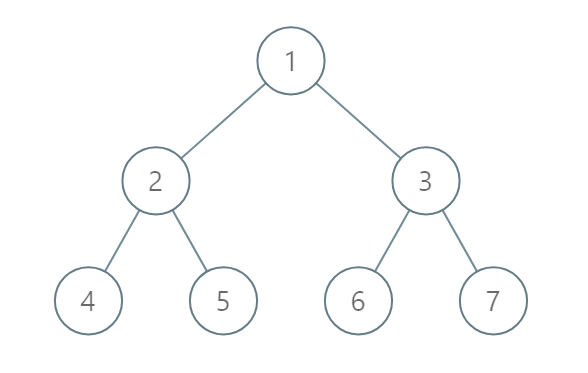
Input: root = [1,2,3,4,5,6,7]
Output: [[4],[2],[1,5,6],[3],[7]]
Explanation: The node with value 5 and the node with value 6 have the same position according to the given scheme.
However, in the report [1,5,6], the node with value 5 comes first since 5 is smaller than 6.

Constraints:

• The number of nodes in the tree is in the range [1, 1000].
• 0 <= Node.val <= 1000

Solution

class Solution {
    typedef struct _node {
        int y;
        int val;
        _node(int y, int val): y(y), val(val) {}
        bool operator<(const _node &a) {
            return this->y > a.y || (this->y == a.y && this->val < a.val);
        }
    } node;
    map<int, vector<node>> result;
    void traversal(TreeNode *root, int x, int y) {
        if(!root) return;
        result[x].push_back(node(y, root->val));
        traversal(root->left, x-1, y-1);
        traversal(root->right, x+1, y-1);
    }
public:
    vector<vector<int>> verticalTraversal(TreeNode* root) {
        traversal(root, 0, 0);
        vector<vector<int>> answer;
        for(auto &[_, nodes] : result) {
            answer.push_back(vector<int>());
            if(nodes.size() == 1) {
                answer.back().push_back(nodes.back().val);
            } else {
                sort(nodes.begin(), nodes.end());
                for(auto &node : nodes) answer.back().push_back(node.val);
            }
        }
        return answer;
    }
};