2021-01-26 Daily-Challenge
Today I have done Sum of Distances in Tree, Convert Sorted List to Binary Search Tree, Rank Teams by Votes and leetcode's January LeetCoding Challenge with cpp.
Sum of Distances in Tree
Description
An undirected, connected tree with N nodes labelled 0...N-1 and N-1 edges are given.
The ith edge connects nodes edges[i][0] and edges[i][1] together.
Return a list ans, where ans[i] is the sum of the distances between node i and all other nodes.
Example 1:
Input: N = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
Output: [8,12,6,10,10,10]
Explanation:
Here is a diagram of the given tree:
0
/ \
1 2
/|\
3 4 5
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8. Hence, answer[0] = 8, and so on.
Note: 1 <= N <= 10000
Solution
tree DP is hard...
class Solution {
vector<int> dp, sz, answer;
vector<vector<int>> neighbors;
void dfs(int current, int parent) {
sz[current] = 1;
for(auto neighbor : neighbors[current]) {
if(neighbor == parent) continue;
dfs(neighbor, current);
dp[current] += dp[neighbor];
dp[current] += sz[neighbor];
sz[current] += sz[neighbor];
}
}
void swapRootDFS(int current, int parent) {
answer[current] = dp[current];
for(auto neighbor : neighbors[current]) {
if(neighbor == parent) continue;
dp[current] -= dp[neighbor] + sz[neighbor];
sz[current] -= sz[neighbor];
dp[neighbor] += dp[current] + sz[current];
sz[neighbor] += sz[current];
swapRootDFS(neighbor, current);
sz[neighbor] -= sz[current];
dp[neighbor] -= dp[current] + sz[current];
sz[current] += sz[neighbor];
dp[current] += dp[neighbor] + sz[neighbor];
}
}
public:
vector<int> sumOfDistancesInTree(int N, vector<vector<int>>& edges) {
dp.resize(N);
sz.resize(N);
answer.resize(N);
neighbors.resize(N);
for(auto &edge : edges) {
neighbors[edge[0]].push_back(edge[1]);
neighbors[edge[1]].push_back(edge[0]);
}
dfs(0, -1);
swapRootDFS(0, -1);
return move(answer);
}
};
Convert Sorted List to Binary Search Tree
Description
Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.
For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
Example 1:
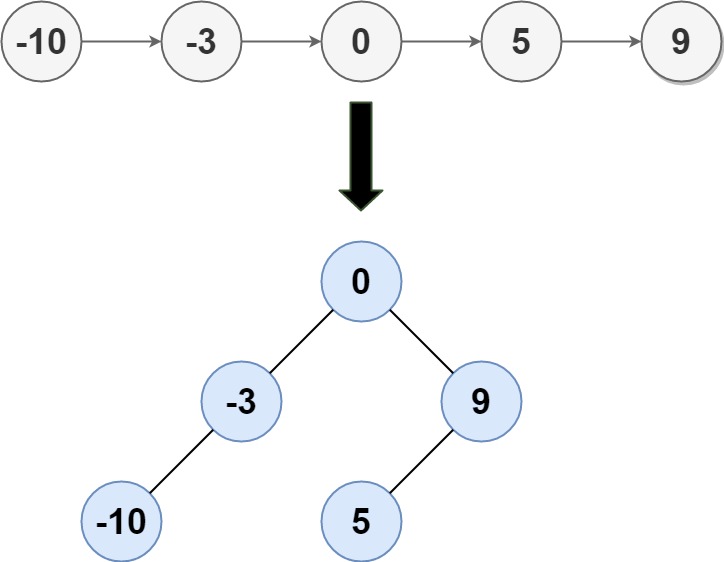
Input: head = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.
Example 2:
Input: head = []
Output: []
Example 3:
Input: head = [0]
Output: [0]
Example 4:
Input: head = [1,3]
Output: [3,1]
Constraints:
- The number of nodes in
headis in the range[0, 2 * 104]. -10^5 <= Node.val <= 10^5
Solution
using more space for shorter code and better time performance
class Solution {
TreeNode *buildBST(vector<int> &vals, int begin, int end) {
if(begin > end) return nullptr;
int mid = (begin + end) / 2;
TreeNode *newRoot = new TreeNode(vals[mid], buildBST(vals, begin, mid-1), buildBST(vals, mid+1, end));
return newRoot;
}
public:
TreeNode* sortedListToBST(ListNode* head) {
if(!head) return nullptr;
vector<int> vals;
while(head) {
vals.push_back(head->val);
head = head->next;
}
return buildBST(vals, 0, vals.size()-1);
}
};
Rank Teams by Votes
Description
In a special ranking system, each voter gives a rank from highest to lowest to all teams participated in the competition.
The ordering of teams is decided by who received the most position-one votes. If two or more teams tie in the first position, we consider the second position to resolve the conflict, if they tie again, we continue this process until the ties are resolved. If two or more teams are still tied after considering all positions, we rank them alphabetically based on their team letter.
Given an array of strings votes which is the votes of all voters in the ranking systems. Sort all teams according to the ranking system described above.
Return a string of all teams sorted by the ranking system.
Example 1:
Input: votes = ["ABC","ACB","ABC","ACB","ACB"]
Output: "ACB"
Explanation: Team A was ranked first place by 5 voters. No other team was voted as first place so team A is the first team.
Team B was ranked second by 2 voters and was ranked third by 3 voters.
Team C was ranked second by 3 voters and was ranked third by 2 voters.
As most of the voters ranked C second, team C is the second team and team B is the third.
Example 2:
Input: votes = ["WXYZ","XYZW"]
Output: "XWYZ"
Explanation: X is the winner due to tie-breaking rule. X has same votes as W for the first position but X has one vote as second position while W doesn't have any votes as second position.
Example 3:
Input: votes = ["ZMNAGUEDSJYLBOPHRQICWFXTVK"]
Output: "ZMNAGUEDSJYLBOPHRQICWFXTVK"
Explanation: Only one voter so his votes are used for the ranking.
Example 4:
Input: votes = ["BCA","CAB","CBA","ABC","ACB","BAC"]
Output: "ABC"
Explanation:
Team A was ranked first by 2 voters, second by 2 voters and third by 2 voters.
Team B was ranked first by 2 voters, second by 2 voters and third by 2 voters.
Team C was ranked first by 2 voters, second by 2 voters and third by 2 voters.
There is a tie and we rank teams ascending by their IDs.
Example 5:
Input: votes = ["M","M","M","M"]
Output: "M"
Explanation: Only team M in the competition so it has the first rank.
Constraints:
1 <= votes.length <= 10001 <= votes[i].length <= 26votes[i].length == votes[j].lengthfor0 <= i, j < votes.length.votes[i][j]is an English upper-case letter.- All characters of
votes[i]are unique. - All the characters that occur in
votes[0]also occur invotes[j]where1 <= j < votes.length.
Solution
just sort, time complexity is $O(n\log n)$ with a large constant.
class Solution {
public:
string rankTeams(vector<string>& votes) {
int cnt[26][26] = {0};
int sLen = votes.front().length();
int len = votes.size();
for(int i = 0; i < len; ++i) {
for(int j = 0; j < sLen; ++j) cnt[votes[i][j]-'A'][j] += 1;
}
string answer = votes.front();
sort(answer.begin(), answer.end(), [&](char a, char b){
int aI = a - 'A';
int bI = b - 'A';
for(int i = 0; i < sLen; ++i) {
if(cnt[aI][i] > cnt[bI][i]) return true;
if(cnt[aI][i] < cnt[bI][i]) return false;
}
return a < b;
});
return answer;
}
};
January LeetCoding Challenge 26
Description
Path With Minimum Effort
You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.
A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.
Return the minimum effort required to travel from the top-left cell to the bottom-right cell.
Example 1:
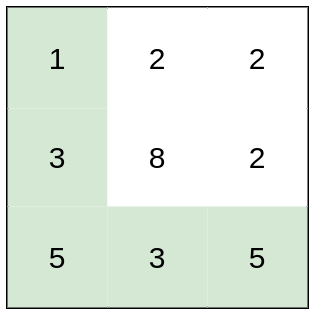
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.
Example 2:
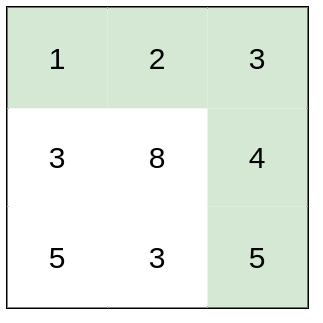
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].
Example 3:
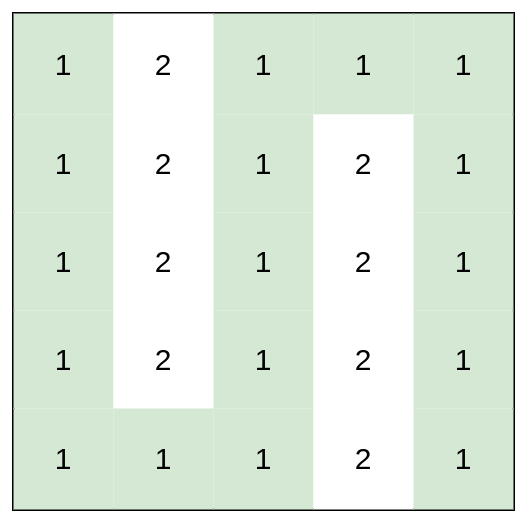
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.
Constraints:
rows == heights.lengthcolumns == heights[i].length1 <= rows, columns <= 1001 <= heights[i][j] <= 106
Solution
why need devide&conquer, time complexity won't be better because large path will take more rounds to walk through the grids.
class Solution {
int moves[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
public:
int minimumEffortPath(vector<vector<int>>& heights) {
typedef pair<int, int> pi;
int rows = heights.size();
int cols = heights.front().size();
vector<vector<bool>> vis(rows, vector<bool>(cols));
auto cmp = [](pair<int, pi> &left, pair<int, pi> &right) { return left.first > right.first; };
priority_queue<pair<int, pi>, vector<pair<int, pi>>, decltype(cmp)> q(cmp);
q.push(make_pair(0, make_pair(0, 0)));
while(!q.empty()) {
auto [effort, pos] = q.top();
q.pop();
auto [row, col] = pos;
cout << effort << ' ' << row << ' ' << col << endl;
if(vis[row][col]) continue;
vis[row][col] = true;
if(row == rows-1 && col == cols-1) return effort;
for(int i = 0; i < 4; ++i) {
int newRow = row + moves[i][0];
int newCol = col + moves[i][1];
if(newRow < 0 || newCol < 0 || newRow >= rows || newCol >= cols || vis[newRow][newCol]) continue;
q.push(make_pair(max(effort, abs(heights[row][col]-heights[newRow][newCol])), make_pair(newRow, newCol)));
}
}
return -1;
}
};