Today is Sunday, I gonna review the tasks I've done this week, and finish today's leetcode's January LeetCoding Challenge with cpp.

BTW, I participated in Weekly Contest 225.

January LeetCoding Challenge 24

Description

Merge k Sorted Lists

You are given an array of k linked-lists lists, each linked-list is sorted in ascending order.

Merge all the linked-lists into one sorted linked-list and return it.

Example 1:

Input: lists = [[1,4,5],[1,3,4],[2,6]]
Output: [1,1,2,3,4,4,5,6]
Explanation: The linked-lists are:
[
  1->4->5,
  1->3->4,
  2->6
]
merging them into one sorted list:
1->1->2->3->4->4->5->6

Example 2:

Input: lists = []
Output: []

Example 3:

Input: lists = [[]]
Output: []

Constraints:

• k == lists.length
• 0 <= k <= 10^4
• 0 <= lists[i].length <= 500
• -10^4 <= lists[i][j] <= 10^4
• lists[i] is sorted in ascending order.
• The sum of lists[i].length won't exceed 10^4.

Solution

class Solution {
    ListNode* merge2Lists(ListNode *a, ListNode *b) {
        ListNode *newHead = new ListNode(-1);
        ListNode *cur = newHead;
        while(a && b) {
            if(a->val < b->val) {
                cur->next = a;
                cur = cur->next;
                a = a->next;
            } else {
                cur->next = b;
                cur = cur->next;
                b = b->next;
            }
        }
        if(a) cur->next = a;
        if(b) cur->next = b;
        return newHead->next;
    }
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        int len = lists.size();
        if(!len) return nullptr;
        for(int i = 1; i < len; i <<= 1) {
            int begin = 0;
            while(begin + i < len) {
                lists[begin] = merge2Lists(lists[begin], lists[begin+i]);
                begin += 2*i;
            }
        }
        return lists[0];
    }
};

Weekly Contest 225

1736. Latest Time by Replacing Hidden Digits

You are given a string time in the form of hh:mm, where some of the digits in the string are hidden (represented by ?).

The valid times are those inclusively between 00:00 and 23:59.

Return the latest valid time you can get from time by replacing the hidden digits.

Example 1:

Input: time = "2?:?0"
Output: "23:50"
Explanation: The latest hour beginning with the digit '2' is 23 and the latest minute ending with the digit '0' is 50.

Example 2:

Input: time = "0?:3?"
Output: "09:39"

Example 3:

Input: time = "1?:22"
Output: "19:22"

Constraints:

• time is in the format hh:mm.
• It is guaranteed that you can produce a valid time from the given string.

Solution

class Solution {
public:
    string maximumTime(string time) {
        if(time[0] == '?' && time[1] == '?') {
            time[0] = '2';
            time[1] = '3';
        } else if (time[0] == '?') {
            if(time[1] > '3') {
                time[0] = '1';
            } else {
                time[0] = '2';
            }
        } else if (time[1] == '?') {
            if(time[0] == '2') {
                time[1] = '3';
            } else {
                time[1] = '9';
            }
        }
        
        if(time[3] == '?') {
            time[3] = '5';
        } 
        if(time[4] == '?') {
            time[4] = '9';
        }
        return move(time);
    }
};

1737. Change Minimum Characters to Satisfy One of Three Conditions

You are given two strings a and b that consist of lowercase letters. In one operation, you can change any character in a or b to any lowercase letter.

Your goal is to satisfy one of the following three conditions:

• Every letter in a is strictly less than every letter in b in the alphabet.
• Every letter in b is strictly less than every letter in a in the alphabet.
• Both a and b consist of only one distinct letter.

Return the minimum number of operations needed to achieve your goal.

Example 1:

Input: a = "aba", b = "caa"
Output: 2
Explanation: Consider the best way to make each condition true:
1) Change b to "ccc" in 2 operations, then every letter in a is less than every letter in b.
2) Change a to "bbb" and b to "aaa" in 3 operations, then every letter in b is less than every letter in a.
3) Change a to "aaa" and b to "aaa" in 2 operations, then a and b consist of one distinct letter.
The best way was done in 2 operations (either condition 1 or condition 3).

Example 2:

Input: a = "dabadd", b = "cda"
Output: 3
Explanation: The best way is to make condition 1 true by changing b to "eee".

Constraints:

• 1 <= a.length, b.length <= 105
• a and b consist only of lowercase letters.

Solution

class Solution {
public:
    int minCharacters(string a, string b) {
        map<char, int> cntA, cntB;
        for(auto c : a) cntA[c] += 1;
        for(auto c : b) cntB[c] += 1;
        int answer = INT_MAX;
        
        for(char c = 'a'; c <= 'z'; ++c) {
            int result1 = 0, result2 = 0;
            for(auto [ch, cnt] : cntA) {
                if(ch <= c) {
                    result1 += cnt;
                } else {
                    result2 += cnt;
                }
            }
            for(auto [ch, cnt] : cntB) {
                if(ch > c) {
                    result1 += cnt;
                } else {
                    result2 += cnt;
                }
            }
            if(c != 'z') answer = min(answer, result1);
            answer = min(answer, result2);
        }
        
        int lenA = a.length(), lenB = b.length();
        for(auto [c, cnt] : cntA) {
            answer = min(answer, lenA+lenB-cnt-cntB[c]);
        }
        for(auto [c, cnt] : cntB) {
            answer = min(answer, lenA+lenB-cnt-cntA[c]);
        }
        
        return answer;
    }
};

1738. Find Kth Largest XOR Coordinate Value

You are given a 2D matrix of size m x n, consisting of non-negative integers. You are also given an integer k.

The value of coordinate (a, b) of the matrix is the XOR of all matrix[i][j] where 0 <= i <= a < m and 0 <= j <= b < n (0-indexed).

Find the kth largest value (1-indexed) of all the coordinates of matrix.

Example 1:

Input: matrix = [[5,2],[1,6]], k = 1
Output: 7
Explanation: The value of coordinate (0,1) is 5 XOR 2 = 7, which is the largest value.

Example 2:

Input: matrix = [[5,2],[1,6]], k = 2
Output: 5
Explanation: The value of coordinate (0,0) is 5 = 5, which is the 2nd largest value.

Example 3:

Input: matrix = [[5,2],[1,6]], k = 3
Output: 4
Explanation: The value of coordinate (1,0) is 5 XOR 1 = 4, which is the 3rd largest value.

Example 4:

Input: matrix = [[5,2],[1,6]], k = 4
Output: 0
Explanation: The value of coordinate (1,1) is 5 XOR 2 XOR 1 XOR 6 = 0, which is the 4th largest value.

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 1000
• 0 <= matrix[i][j] <= 106
• 1 <= k <= m * n

Solution

class Solution {
public:
    int kthLargestValue(vector<vector<int>>& matrix, int k) {
        int m = matrix.size();
        int n = matrix.front().size();
        vector<vector<int>> coordinate(m, vector<int>(n));
        vector<int> coordinates;
        for(int i = 0; i < m; ++i) {
            for(int j = 0; j < n; ++j) {
                coordinate[i][j] = matrix[i][j];
                if(j) coordinate[i][j] ^= coordinate[i][j-1];
                if(i) coordinate[i][j] ^= coordinate[i-1][j];
                if(i && j) coordinate[i][j] ^= coordinate[i-1][j-1];
                coordinates.push_back(coordinate[i][j]);
            }
        }
        nth_element(coordinates.begin(), coordinates.begin()+k-1, coordinates.end(), greater<int>());
        return coordinates[k-1];
    }
};

1739. Building Boxes

You have a cubic storeroom where the width, length, and height of the room are all equal to n units. You are asked to place n boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:

• You can place the boxes anywhere on the floor.
• If box x is placed on top of the box y, then each side of the four vertical sides of the box y must either be adjacent to another box or to a wall.

Given an integer n, return the minimum possible number of boxes touching the floor.

Example 1:

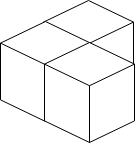
Input: n = 3
Output: 3
Explanation: The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.

Example 2:

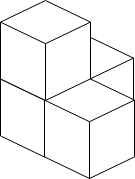
Input: n = 4
Output: 3
Explanation: The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.

Example 3:

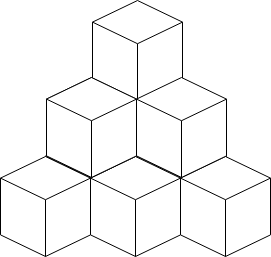
Input: n = 10
Output: 6
Explanation: The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.

Constraints:

• 1 <= n <= 109

Solution

by observing the following table

box number	answer
1	1
2	2
3	3
4	3
5	4
6	5
7	5
8	6
9	6
10	6
11	7
12	8
13	8
14	9
15	9
16	9
17	10
18	10
19	10
20	10
21	11

I found that same result occurs at intervals of length of 1, 1, 2, 1, 2, 3,..., 1, 2, ..., k.

So for a input n, I should find the max k that sum of them is less or equal to n. and sum of them are $\frac{k\times(k-1)\times(k-2)}{6}$. then I can brute force to find where n stop at next iteration.

class Solution {
    long long cubsum(long long a) {
        return a*(a+1)*(a+2)/6;
    }
public:
    int minimumBoxes(int n) {
        // larger upper bound will cause cubsum overflow long long
        // and 1e5 is large enough that cubsum(1e5) is definitely
        // greater than n
        long long end = 1e5;
        end = min(end, 1LL*n);
        long long begin = 0;
        while(begin < end) {
            long long mid = (begin + end) / 2;
            if(cubsum(mid) < n) {
                begin = mid + 1;
            } else {
                end = mid;
            }
        }
        if(cubsum(begin) > n) begin -= 1;
        // cout << begin << ' ' << cubsum(begin) << endl;
        int answer = 0;
        for(int i = 1; i <= begin; ++i) {
            answer += i;
        }
        int rest = n - cubsum(begin), count = 1;
        while(rest > 0) {
            rest -= count;
            count += 1;
            answer += 1;
        }
        return answer;
    }
};