Today I have done Copy List with Random Pointer, LRU Cache and leetcode's January LeetCoding Challenge with cpp.

Copy List with Random Pointer

Description

A linked list is given such that each node contains an additional random pointer which could point to any node in the list or null.

Return a deep copy of the list.

The Linked List is represented in the input/output as a list of n nodes. Each node is represented as a pair of [val, random_index] where:

• val: an integer representing Node.val
• random_index: the index of the node (range from 0 to n-1) where random pointer points to, or null if it does not point to any node.

Example 1:

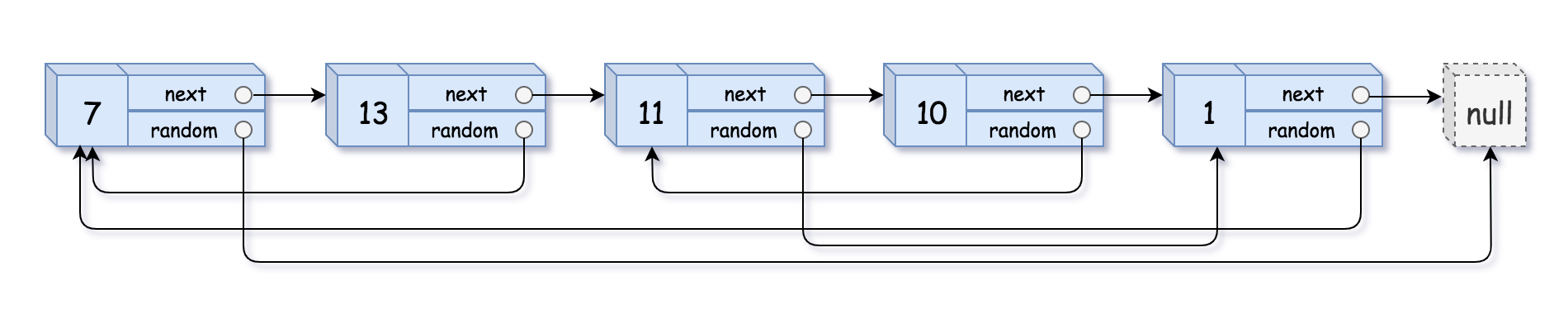
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]

Example 2:

Input: head = [[1,1],[2,1]]
Output: [[1,1],[2,1]]

Example 3:

Input: head = [[3,null],[3,0],[3,null]]
Output: [[3,null],[3,0],[3,null]]

Example 4:

Input: head = []
Output: []
Explanation: Given linked list is empty (null pointer), so return null.

Constraints:

• -10000 <= Node.val <= 10000
• Node.random is null or pointing to a node in the linked list.
• The number of nodes will not exceed 1000.

Solution

use a unordered_map

class Solution {
public:
    Node* copyRandomList(Node* head) {
        Node *newHead = new Node(-1);
        Node *cur = newHead;
        unordered_map<Node*, Node*> mp;
        while(head) {
            cur->next = new Node(head->val);
            mp[head] = cur->next;
            cur = cur->next;
            cur->random = head->random;
            head = head->next;
        }
        mp[NULL] = NULL;
        cur = newHead->next;
        while(cur) {
            cur->random = mp[cur->random];
            cur = cur->next;
        }
        return newHead->next;
    }
};

LRU Cache

Description

Design a data structure that follows the constraints of a Least Recently Used (LRU) cache.

Implement the LRUCache class:

• LRUCache(int capacity) Initialize the LRU cache with positive size capacity.
• int get(int key) Return the value of the key if the key exists, otherwise return -1.
• void put(int key, int value) Update the value of the key if the key exists. Otherwise, add the key-value pair to the cache. If the number of keys exceeds the capacity from this operation, evict the least recently used key.

Follow up: Could you do get and put in O(1) time complexity?

Example 1:

Input
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
Output
[null, null, null, 1, null, -1, null, -1, 3, 4]

Explanation
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1);    // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2);    // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1);    // return -1 (not found)
lRUCache.get(3);    // return 3
lRUCache.get(4);    // return 4

Constraints:

• 1 <= capacity <= 3000
• 0 <= key <= 3000
• 0 <= value <= 104
• At most 3 * 104 calls will be made to get and put.

Solution

use a list and two unordered_map

code can be more elegant

class LRUCache {
    int capacity;
    list<int> LRU;
    unordered_map<int, list<int>::iterator> position;
    unordered_map<int, int> kv;
public:
    LRUCache(int capacity) : capacity(capacity) {}
    
    int get(int key) {
        if(kv.count(key)) {
            LRU.erase(position[key]);
            LRU.push_front(key);
            position[key] = LRU.begin();
            return kv[key];
        }
        return -1;
    }
    
    void put(int key, int value) {
        if(kv.count(key)) {
            LRU.erase(position[key]);
        } else {
            if(kv.size() == capacity) {
                kv.erase(LRU.back());
                position.erase(LRU.back());
                LRU.pop_back();
            }
        }
        LRU.push_front(key);
        position[key] = LRU.begin();
        kv[key] = value;
    }
};

January LeetCoding Challenge 14

Description

Minimum Operations to Reduce X to Zero

You are given an integer array nums and an integer x. In one operation, you can either remove the leftmost or the rightmost element from the array nums and subtract its value from x. Note that this modifies the array for future operations.

Return the minimum number of operations to reduce x to exactly 0 if it's possible*, otherwise, return* -1.

Example 1:

Input: nums = [1,1,4,2,3], x = 5
Output: 2
Explanation: The optimal solution is to remove the last two elements to reduce x to zero.

Example 2:

Input: nums = [5,6,7,8,9], x = 4
Output: -1

Example 3:

Input: nums = [3,2,20,1,1,3], x = 10
Output: 5
Explanation: The optimal solution is to remove the last three elements and the first two elements (5 operations in total) to reduce x to zero.

Constraints:

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 104
• 1 <= x <= 109

Solution

class Solution {
public:
    int minOperations(vector<int>& nums, int x) {
        int len = nums.size();
        int sum = 0;
        unordered_map<int, int> sumLeft, sumRight;
        int pos = 0;
        while(pos < len && sum < x) {
            sum += nums[pos];
            sumLeft[sum] = pos;
            pos += 1;
        }
        pos = len-1;
        sum = 0;
        while(pos >= 0 && sum < x) {
            sum += nums[pos];
            sumRight[sum] = pos;
            pos -= 1;
        }
        int answer = INT_MAX;
        for(auto [sum, pos] : sumLeft) {
            if(sumRight.count(x-sum) && sumRight[x-sum] > pos) answer = min(answer, pos + 1 + len - sumRight[x-sum]);
        }
        if(sumLeft.count(x)) answer = min(answer, sumLeft[x] + 1);
        if(sumRight.count(x)) answer = min(answer, len - sumRight[x]);
        return answer == INT_MAX ? -1 : answer;
    }
};