Today I have done Lowest Common Ancestor of a Binary Tree on leetcode and leetcode's December LeetCoding Challenge with cpp.

Lowest Common Ancestor of a Binary Tree

Description

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [1,2], p = 1, q = 2
Output: 1

Constraints:

• The number of nodes in the tree is in the range [2, 105].
• -109 <= Node.val <= 109
• All Node.val are unique.
• p != q
• p and q will exist in the tree.

Solution

inorder traversal, when we reach first node, we keep tracking of highest node till we find another node, then that node is the answer.

class Solution {
    TreeNode *answer;
    bool findLeft;
    int level;
    
    bool helper(TreeNode *root, int level, TreeNode *p, TreeNode *q) {
        if(!root) return false;
        if(helper(root->left, level+1, p, q)) return true;
        if(findLeft){
            if(level < this->level) {
                answer = root;
                this->level = level;
            }
            if(root == p || root == q) return true;
        } else if(root == p || root == q) {
            findLeft = true;
            answer = root;
            this->level = level;
        }
        if(helper(root->right, level+1, p, q)) return true;
        return false;
    }
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        helper(root, 0, p, q);
        return answer;
    }
};

December LeetCoding Challenge 29

Description

Reach a Number

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

Example 1:

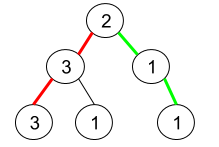
Input: root = [2,3,1,3,1,null,1]
Output: 2 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 2:

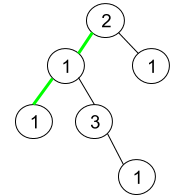
Input: root = [2,1,1,1,3,null,null,null,null,null,1]
Output: 1 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 3:

Input: root = [9]
Output: 1

Constraints:

• The given binary tree will have between 1 and 10^5 nodes.
• Node values are digits from 1 to 9.

Solution

just need to statistics number of odd-amount-digit

class Solution {
    bool parity[10] = {0};
    int answer = 0;
    int odd = 0;
    void helper(TreeNode *root) {
        parity[root->val] ^= 1;
        if(parity[root->val]) odd += 1;
        else odd -= 1;
        if(!(root->left) && !(root->right)) answer += (odd < 2);
        if(root->left) helper(root->left);
        if(root->right) helper(root->right);
        if(parity[root->val]) odd -= 1;
        else odd += 1;
        parity[root->val] ^= 1;
    }
public:
    int pseudoPalindromicPaths (TreeNode* root) {
        helper(root);
        return answer;
    }
};