Today I have done Merge Two Sorted Lists on leetcode and leetcode's December LeetCoding Challenge with cpp.

Merge Two Sorted Lists

Description

Merge two sorted linked lists and return it as a new sorted list. The new list should be made by splicing together the nodes of the first two lists.

Example 1:

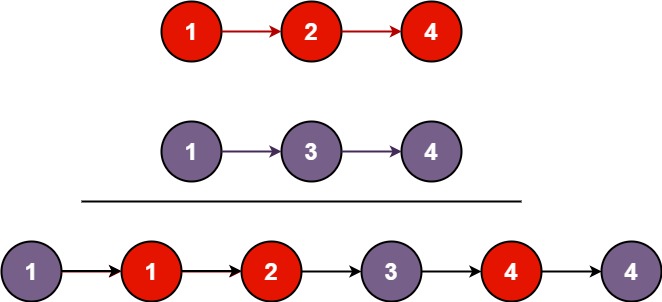
Input: l1 = [1,2,4], l2 = [1,3,4]
Output: [1,1,2,3,4,4]

Example 2:

Input: l1 = [], l2 = []
Output: []

Example 3:

Input: l1 = [], l2 = [0]
Output: [0]

Constraints:

• The number of nodes in both lists is in the range [0, 50].
• -100 <= Node.val <= 100
• Both l1 and l2 are sorted in non-decreasing order.

Solution

nothing to say

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        ListNode *newHead = new ListNode();
        ListNode *cur = newHead;
        while(l1 && l2) {
            if(l1->val < l2->val) {
                cur->next = l1;
                l1 = l1->next;
            } else {
                cur->next = l2;
                l2 = l2->next;
            }
            cur = cur->next;
        }
        if(l1) cur->next = l1;
        if(l2) cur->next = l2;
        return newHead->next;
    }
};

December LeetCoding Challenge 28

Description

Reach a Number

You are standing at position 0 on an infinite number line. There is a goal at position target.

On each move, you can either go left or right. During the n-th move (starting from 1), you take n steps.

Return the minimum number of steps required to reach the destination.

Example 1:

Input: target = 3
Output: 2
Explanation:
On the first move we step from 0 to 1.
On the second step we step from 1 to 3.

Example 2:

Input: target = 2
Output: 3
Explanation:
On the first move we step from 0 to 1.
On the second move we step  from 1 to -1.
On the third move we step from -1 to 2.

Note:

target will be a non-zero integer in the range [-10^9, 10^9].

Solution

we can just think that target is a positive integer, because we are on a infinite number line and we can go both directions at any time, so we can reach -n with same moves as n, just take every moves to opposite direction.

at first, I find that we can use two moves to step exactly 1. so I think I can find the moves n where n*(n+1)/2(farthest position by n moves), and find how many moves I need to achieve target.

which is wrong solution XD

because we can go back at any time, so optimal solution is go back at the right move. it's obviously that if we reverse one move, we will go back at a even number. which means simply reverse moves won't change parity of position by specified moves, so we may need to take at most two steps forward.

so here's our solution:

• find n where n is smallest positive number that $\frac{n*n(+1)}{2}\ge target$
• if $\frac{n*n(+1)}{2} = target$, n is answer
  • if $\frac{nn(+1)}{2} > target$ and $\frac{nn(+1)}{2} - target$ is even, n is still answer, we'll take a negative move when it comes to $\frac{\frac{n*n(+1)}{2} - target}{2}$th move
  • if $\frac{nn(+1)}{2} > target$ and $\frac{nn(+1)}{2} - target$ is odd:
    • if n is even, we take one more step forward, and take a negative move at $\frac{\frac{n*n(+1)}{2} - target + n+1}{2}$th move
    • if n is odd, we take one more step forward, and take two negative move where their sum is $\frac{\frac{n*n(+1)}{2} - target + n+1+n+2}{2}$.

class Solution {
public:
    int reachNumber(int target) {
        target = abs(target);
        int start = 1, end = 45555;
        while(start < end) {
            int mid = (start + end) / 2;
            int pos = mid * (mid + 1) / 2;
            if(pos < target) {
                start = mid + 1;
            } else {
                end = mid;
            }
        }
        int answer = start;
        int diff = abs(target - start * (start + 1) / 2);
        if(diff & 1) {
            answer += 1 + ((start&1)^1);
        }
        return answer;
    }
};