Today I have done Sort the Matrix Diagonally and Merge k Sorted Lists on leetcode and leetcode's December LeetCoding Challenge with cpp.

Sort the Matrix Diagonally

Description

Given a m * n matrix mat of integers, sort it diagonally in ascending order from the top-left to the bottom-right then return the sorted array.

Example 1:

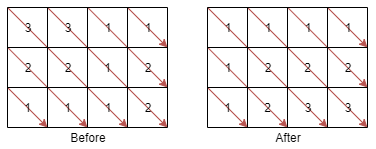
Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
Output: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• 1 <= mat[i][j] <= 100

Solution

this problem is so... disgusting

class Solution {
public:
    vector<vector<int>> diagonalSort(vector<vector<int>>& mat) {
        int h = mat.size();
        int w = mat[0].size();
        vector<int> index;
        for(int i = 0; i < h+w-1; ++i) {
            int beginH = i >= w ? i-w+1 : 0;
            int endH = beginH ? (i+w-1 < h ? i+w-1 : h-1) : min(i, h-1);
            // cout << beginH << ' ' << endH << endl;
            if(beginH == endH) continue;
            index.clear();
            for(int j = beginH; j <= endH; ++j) {
                index.push_back(mat[j][j+w-1-i]);
            }
            sort(index.begin(), index.end());
            for(int j = beginH; j <= endH; ++j) {
                mat[j][j+w-1-i] = index[j-beginH];
            }
        }
        return mat;
    }
};

Merge k Sorted Lists

Description

You are given an array of k linked-lists lists, each linked-list is sorted in ascending order.

Merge all the linked-lists into one sorted linked-list and return it.

Example 1:

Input: lists = [[1,4,5],[1,3,4],[2,6]]
Output: [1,1,2,3,4,4,5,6]
Explanation: The linked-lists are:
[
  1->4->5,
  1->3->4,
  2->6
]
merging them into one sorted list:
1->1->2->3->4->4->5->6

Example 2:

Input: lists = []
Output: []

Example 3:

Input: lists = [[]]
Output: []

Constraints:

• k == lists.length
• 0 <= k <= 10^4
• 0 <= lists[i].length <= 500
• -10^4 <= lists[i][j] <= 10^4
• lists[i] is sorted in ascending order.
• The sum of lists[i].length won't exceed 10^4.

Solution

nothing to say

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        priority_queue<ListNode*, vector<ListNode*>, bool(*)(ListNode*, ListNode*)> q([](ListNode* a, ListNode* b){
            return a->val > b->val;
        });
        if(lists.empty()) return nullptr;
        ListNode* newHead = new ListNode(-100100);
        ListNode* cur = newHead;
        for(auto list: lists) {
            if(list) q.push(list);
        }
        while(q.size()) {
            cur->next = q.top();
            q.pop();
            cur = cur->next;
            if(cur->next) q.push(cur->next);
        }
        return newHead->next;
    }
};

December LeetCoding Challenge 3

Description

Increasing Order Search Tree

Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.

Example 1:

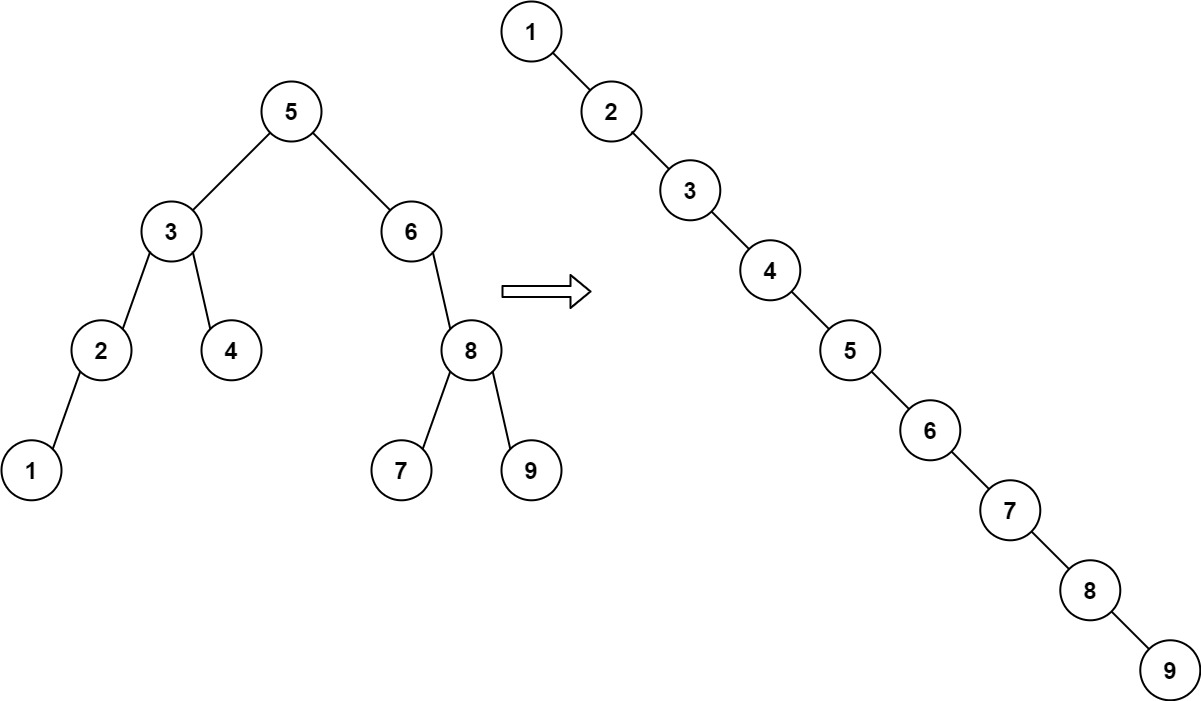
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

Example 2:

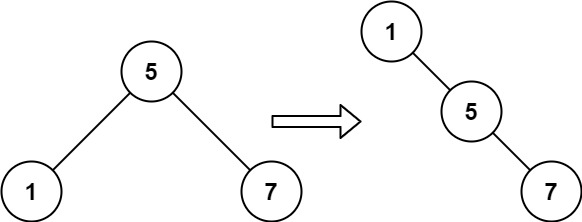
Input: root = [5,1,7]
Output: [1,null,5,null,7]

Constraints:

• The number of nodes in the given tree will be in the range [1, 100].
• 0 <= Node.val <= 1000

Solution

inorder traversal is all we need, 'cause it's a BST

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    void helper(TreeNode* root, TreeNode* &newRoot) {
        if(!root) return;
        helper(root->left, newRoot);
        newRoot->right = new TreeNode(root->val);
        newRoot = newRoot->right;
        helper(root->right, newRoot);
    }
public:
    TreeNode* increasingBST(TreeNode* root) {
        TreeNode* newRootHead = new TreeNode(-1);
        TreeNode* helperNode = newRootHead;
        helper(root, helperNode);
        return newRootHead->right;
    }
};