Today I have done Unique Paths II and Substring with Concatenation of All Words on leetcode and leetcode's December LeetCoding Challenge with cpp.

Unique Paths II

Description

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and space is marked as 1 and 0 respectively in the grid.

Example 1:

Input: obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
Output: 2
Explanation: There is one obstacle in the middle of the 3x3 grid above.
There are two ways to reach the bottom-right corner:
1. Right -> Right -> Down -> Down
2. Down -> Down -> Right -> Right

Example 2:

Input: obstacleGrid = [[0,1],[0,0]]
Output: 1

Constraints:

• m == obstacleGrid.length
• n == obstacleGrid[i].length
• 1 <= m, n <= 100
• obstacleGrid[i][j] is 0 or 1.

Solution

basic dp

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size(), n = obstacleGrid[0].size();
        if(obstacleGrid[0][0] || obstacleGrid[m-1][n-1]) return 0;
        vector<int> dp(m*n);
        dp[0] = 1;
        for(int i = 1; i < m*n; ++i) {
            if(obstacleGrid[i/n][i%n] == 1) continue;
            if(i >= n) dp[i] += dp[i-n];
            if(i % n != 0) dp[i] += dp[i-1];
        }
        return dp.back();
    }
};

Substring with Concatenation of All Words

Description

You are given a string s and an array of strings words of the same length. Return all starting indices of substring(s) in s that is a concatenation of each word in words exactly once, in any order, and without any intervening characters.

You can return the answer in any order.

Example 1:

Input: s = "barfoothefoobarman", words = ["foo","bar"]
Output: [0,9]
Explanation: Substrings starting at index 0 and 9 are "barfoo" and "foobar" respectively.
The output order does not matter, returning [9,0] is fine too.

Example 2:

Input: s = "wordgoodgoodgoodbestword", words = ["word","good","best","word"]
Output: []

Example 3:

Input: s = "barfoofoobarthefoobarman", words = ["bar","foo","the"]
Output: [6,9,12]

Constraints:

• 1 <= s.length <= $10^4$
• s consists of lower-case English letters.
• 1 <= words.length <= 5000
• 1 <= words[i].length <= 30
• words[i] consists of lower-case English letters.

Solution

first of all, we use s, n, m present length of string, amount of words, length of words.

if we know where every possible word begin, we can solve problem easily and quickly, so we should consider how to compute them quickly.

if we use brute force, time complexity is because amount of words is $O(s\times n\times m)$, worst case there will be about 1e9 times computing so it's not acceptable.

but n is small, so if we use KMP to get start positions, time complexity will be $O(m\times max(s, m))$

when we got start positions, problem becomes easy, we just check every start positions if it is a valid start position for substring.

class Solution {
  vector<int> kmpNext;
  void initNext(string &s) {
    kmpNext.clear();
    kmpNext.push_back(-1);
    int cur = 0;
    int len = s.length();
    for(int i = 1; i < len; ++i) {
      if(cur >= 0 && s[i] == s[cur]) {
      kmpNext.push_back(kmpNext[cur]);
      } else {
      kmpNext.push_back(cur);
        do {
          cur = kmpNext[cur];
        } while(cur >= 0 && s[i] != s[cur]);
      }
      cur += 1;
    }
    kmpNext.push_back(cur);
  }
public:
  vector<int> findSubstring(string s, vector<string>& words) {
    int amount = words.size();
    int len = words[0].length();
    int slen = s.length();
    map<string, int> cnt;
    map<int, string> invertedIndex;
    for(auto &word : words) {
      if(!cnt.count(word)) {
        initNext(word);
        int cur = 0;
        int j = 0;
        while(j < slen) {
          if(s[j] == word[cur]) {
            j += 1;
            cur += 1;
            if(cur == len) {
              invertedIndex[j-cur] = word;
              cur = kmpNext[cur];
            }
          } else {
            cur = kmpNext[cur];
            if(cur < 0) {
              j += 1;
              cur += 1;
            }
          }
        }
      }
      cnt[word] += 1;
    }
    vector<int> answer;
    for(auto &[pos, word] : invertedIndex) {
      if(pos + amount*len > slen) break;
      auto curCnt = cnt;
      int curPos = pos + len;
      curCnt[word] -= 1;
      int rest = amount - 1;
      while(rest && invertedIndex.count(curPos) && curCnt[invertedIndex[curPos]]) {
        curCnt[invertedIndex[curPos]] -= 1;
        rest -= 1;
        curPos += len;
      }
      if(!rest) answer.push_back(pos);
    }
    return answer;
  }
};

December LeetCoding Challenge 1

Description

Maximum Depth of Binary Tree

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

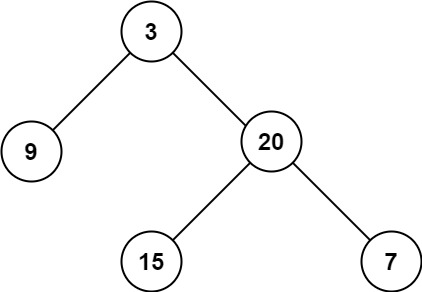
Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Example 3:

Input: root = []
Output: 0

Example 4:

Input: root = [0]
Output: 1

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• -100 <= Node.val <= 100

Solution

nothing to say

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        return root ? 1 + max(maxDepth(root->left), maxDepth(root->right)) : 0;
    }
};