Today I have done Course Schedule IV on leetcode and leetcode's November LeetCoding Challenge with cpp.

Course Schedule IV

Description

There are a total of n courses you have to take, labeled from 0 to n-1.

Some courses may have direct prerequisites, for example, to take course 0 you have first to take course 1, which is expressed as a pair: [1,0]

Given the total number of courses n, a list of direct prerequisite pairs and a list of queries pairs.

You should answer for each queries[i] whether the course queries[i][0] is a prerequisite of the course queries[i][1] or not.

Return a list of boolean, the answers to the given queries.

Please note that if course a is a prerequisite of course b and course b is a prerequisite of course c, then, course a is a prerequisite of course c.

Example 1:

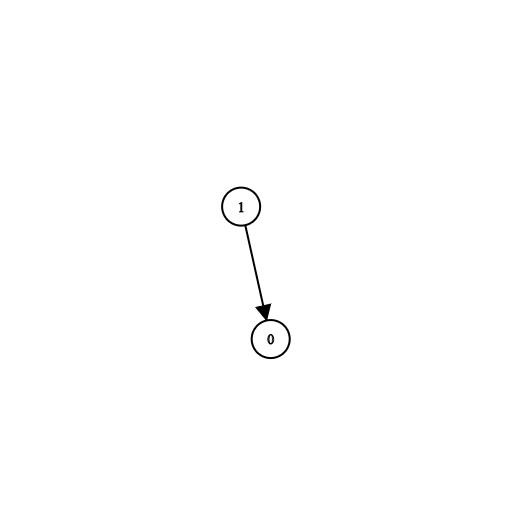
Input: n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
Output: [false,true]
Explanation: course 0 is not a prerequisite of course 1 but the opposite is true.

Example 2:

Input: n = 2, prerequisites = [], queries = [[1,0],[0,1]]
Output: [false,false]
Explanation: There are no prerequisites and each course is independent.

Example 3:

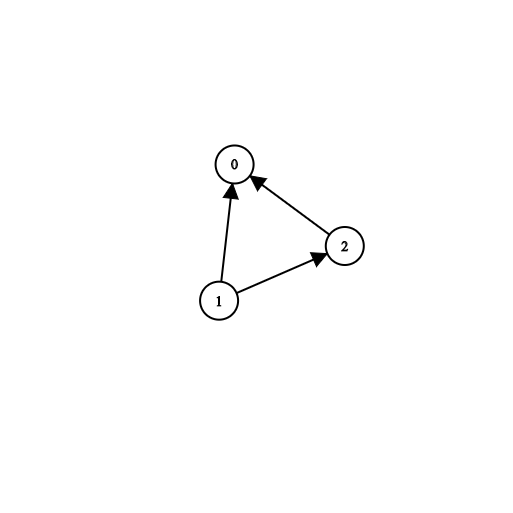
Input: n = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
Output: [true,true]

Example 4:

Input: n = 3, prerequisites = [[1,0],[2,0]], queries = [[0,1],[2,0]]
Output: [false,true]

Example 5:

Input: n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], queries = [[0,4],[4,0],[1,3],[3,0]]
Output: [true,false,true,false]

Constraints:

• 2 <= n <= 100
• 0 <= prerequisite.length <= (n * (n - 1) / 2)
• 0 <= prerequisite[i][0], prerequisite[i][1] < n
• prerequisite[i][0] != prerequisite[i][1]
• The prerequisites graph has no cycles.
• The prerequisites graph has no repeated edges.
• 1 <= queries.length <= 10^4
• queries[i][0] != queries[i][1]

Solution

not so elegant

class Solution {
  vector<vector<bool>> isPrerequisite;
  vector<vector<int>> followUp;
  vector<int> inDegree;
  vector<int> topologicalSort(int n, vector<vector<int>>& prerequisites) {
    inDegree.resize(n);
    fill(inDegree.begin(), inDegree.end(), 0);
    for(auto &p : prerequisites) {
      inDegree[p[1]] += 1;
    }
    queue<int> q;
    for(int i = 0; i < n; ++i) {
      if(inDegree[i] == 0) {
        q.push(i);
      }
    }
    vector<int> result;
    while(q.size()) {
      int cur = q.front();
      q.pop();
      result.push_back(cur);
      for(auto follow: followUp[cur]) {
        inDegree[follow] -= 1;
        if(inDegree[follow] == 0) q.push(follow);
      }
    }
    return result;
  }
  void init(int n, vector<vector<int>>& prerequisites) {
    followUp.resize(n);
    isPrerequisite.resize(n, vector<bool>(n));
    for(auto &p : prerequisites) {
      followUp[p[0]].push_back(p[1]);
    }
  }
public:
  vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
    init(n, prerequisites);
    auto sortedCourse = topologicalSort(n, prerequisites);
    for(auto course : sortedCourse) {
      for(auto follow : followUp[course]) {
        for(int i = 0; i < n; ++i) {
          isPrerequisite[follow][i] = isPrerequisite[follow][i] | isPrerequisite[course][i];
        }
        isPrerequisite[follow][course] = true;
      }
    }

    vector<bool> answer;
    for(auto &query : queries) {
      answer.push_back(isPrerequisite[query[1]][query[0]]);
    }
    return answer;
  }
};

November LeetCoding Challenge 20

Description

Search in Rotated Sorted Array II

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,0,1,2,2,5,6] might become [2,5,6,0,0,1,2]).

You are given a target value to search. If found in the array return true, otherwise return false.

Example 1:

Input: nums = [2,5,6,0,0,1,2], target = 0
Output: true

Example 2:

Input: nums = [2,5,6,0,0,1,2], target = 3
Output: false

Follow up:

• This is a follow up problem to Search in Rotated Sorted Array, where nums may contain duplicates.
• Would this affect the run-time complexity? How and why?

Solution

follow up:

• I don't feel the affect.

class Solution {
public:
    bool search(vector<int>& nums, int target) {
        if(nums.empty()) return false;
        int offset = 0, len = nums.size();
        for(int i = 1; i < len; ++i) {
            if(nums[i] < nums[i-1]) {
                offset = i;
            }
        }
        int start = 0, end = len - 1;
        while(start < end) {
            int mid = (start + end) / 2;
            int pos = (mid + offset) % len;
            if(nums[pos] < target) {
                start = mid + 1;
            } else {
                end = mid;
            }
        }
        int pos = (end + offset) % len;
        return nums[pos] == target;
    }
};