Today I have done Powerful Integers on leetcode and leetcode's November LeetCoding Challenge with cpp.

Powerful Integers

Description

Given two positive integers x and y, an integer is powerful if it is equal to x^i + y^j for some integers i >= 0 and j >= 0.

Return a list of all powerful integers that have value less than or equal to bound.

You may return the answer in any order. In your answer, each value should occur at most once.

Example 1:

Input: x = 2, y = 3, bound = 10
Output: [2,3,4,5,7,9,10]
Explanation: 
2 = 2^0 + 3^0
3 = 2^1 + 3^0
4 = 2^0 + 3^1
5 = 2^1 + 3^1
7 = 2^2 + 3^1
9 = 2^3 + 3^0
10 = 2^0 + 3^2

Example 2:

Input: x = 3, y = 5, bound = 15
Output: [2,4,6,8,10,14]

Note:

• 1 <= x <= 100
• 1 <= y <= 100
• 0 <= bound <= 10^6

Solution

I first write slow but AC answer

class Solution {
public:
    vector<int> powerfulIntegers(int x, int y, int bound) {
        unordered_set<int> xp, yp;
        int cur = 1;
        while(cur < bound && !xp.count(cur)) {
            xp.insert(cur);
            cur *= x;
        }
        cur = 1;
        while(cur < bound && !yp.count(cur)) {
            yp.insert(cur);
            cur *= y;
        }
        vector<int> answer;
        for(int i = 2; i <= bound; ++i) {
            bool powerful = false;
            if(xp.size() < yp.size()) {
                for(auto x : xp) {
                    if(yp.count(i-x)) {
                        powerful = true;
                        break;
                    }
                }
            } else {
                for(auto y : yp) {
                    if(xp.count(i-y)) {
                        powerful = true;
                        break;
                    }
                }
            }
            if(powerful) answer.push_back(i);
        }
        return answer;
    }
};

then I knew that I made a mistake

class Solution {
public:
    vector<int> powerfulIntegers(int x, int y, int bound) {
        unordered_set<int> xp, yp;
        int cur = 1;
        while(cur < bound && !xp.count(cur)) {
            xp.insert(cur);
            cur *= x;
        }
        cur = 1;
        while(cur < bound && !yp.count(cur)) {
            yp.insert(cur);
            cur *= y;
        }
        unordered_set<int> answer;
        for(auto x : xp) {
            for(auto y : yp) {
                if(x+y <= bound) answer.insert(x+y);
            }
        }
        return vector<int>(answer.begin(), answer.end());
    }
};

November LeetCoding Challenge 9

Description

Maximum Difference Between Node and Ancestor

Given the root of a binary tree, find the maximum value V for which there exist different nodes A and B where V = |A.val - B.val| and A is an ancestor of B.

A node A is an ancestor of B if either: any child of A is equal to B, or any child of A is an ancestor of B.

Example 1:

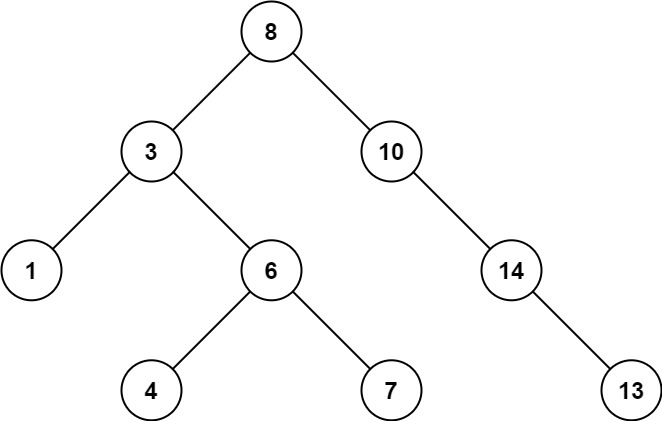
Input: root = [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation: We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.

Example 2:

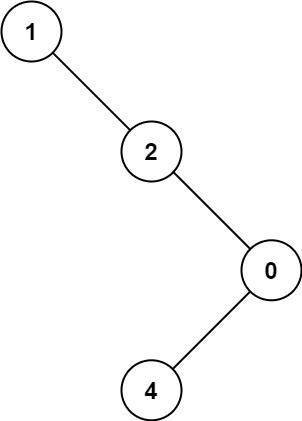
Input: root = [1,null,2,null,0,3]
Output: 3

Constraints:

• The number of nodes in the tree is in the range [2, 5000].
• 0 <= Node.val <= 105

Solution

not a elegant solution

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    tuple<int, int, int> maxDiff(TreeNode* root) {
        int minChild = INT_MAX;
        int maxChild = INT_MIN;
        int diff = 0;
        if(root->left) {
            auto [minLeft, maxLeft, diffLeft] = maxDiff(root->left);
            minChild = min(minLeft, minChild);
            maxChild = max(maxLeft, maxChild);
            diff = max(diff, diffLeft);
            if(minChild != INT_MAX) diff = max(diff, abs(root->val - minLeft));
            if(maxChild != INT_MIN) diff = max(diff, abs(root->val - maxLeft));
        }
        if(root->right) {
            auto [minRight, maxRight, diffRight] = maxDiff(root->right);
            minChild = min(minRight, minChild);
            maxChild = max(maxRight, maxChild);
            diff = max(diff, diffRight);
            if(minChild != INT_MAX) diff = max(diff, abs(root->val - minRight));
            if(maxChild != INT_MIN) diff = max(diff, abs(root->val - maxRight));
        }
        return make_tuple(min(root->val, minChild), max(root->val, maxChild), diff);
        
    }
public:
    int maxAncestorDiff(TreeNode* root) {
        auto [minNode, maxNode, diff] = maxDiff(root);
        return diff;
    }
};