Today is Sunday, I gonna review the tasks I've done this week, and finish today's leetcode's November LeetCoding Challenge with cpp.

BTW I decided to write solution directly on website rather than on VSCode when reviewing.

LeetCode Review

Minimum Height Trees

BFS by degree

class Solution {
    vector<unordered_set<int>> neighbors;
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        if(n == 1) return vector<int>{0};
        neighbors = vector<unordered_set<int>>(n);
        for(auto &edge : edges) {
            neighbors[edge[0]].insert(edge[1]);
            neighbors[edge[1]].insert(edge[0]);
        }
        vector<int> current, next;
        for(int i = 0; i < n; ++i) {
            if(neighbors[i].size() == 1) {
                next.push_back(i);
            }
        }
        while(next.size()) {
            current = next;
            next.clear();
            for(auto n : current) {
                for(auto neighbor : neighbors[n]) {
                    neighbors[neighbor].erase(n);
                    if(neighbors[neighbor].size() == 1) next.push_back(neighbor);
                }
            }
        }
        return current;
    }
};

tree DP

class Solution {
    vector<int> height1, height2, dp;
    vector<vector<int>> neighbors;
    
    void heightDFS(int current, int parent) {
        height1[current] = height2[current] = -1;
        for(auto neighbor : neighbors[current]) {
            if(neighbor == parent) continue;
            heightDFS(neighbor, current);
            int heightFromNeighbor = height1[neighbor] + 1;
            if(heightFromNeighbor > height1[current]) {
                height2[current] = height1[current];
                height1[current] = heightFromNeighbor;
            } else if (heightFromNeighbor > height2[current]) {
                height2[current] = heightFromNeighbor;
            }
        }
        height1[current] = max(height1[current], 0);
    }
    
    void treeDP(int current, int parent, int acc) {
        dp[current] = max(height1[current], acc);
        for(auto neighbor : neighbors[current]) {
            if(neighbor == parent) continue;
            int newAcc = max(acc+1, (height1[neighbor] + 1 == height1[current] ? height2[current]: height1[current]) + 1);
            treeDP(neighbor, current, newAcc);
        }
    }
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        height1.resize(n, 0);
        height2.resize(n, 0);
        dp.resize(n, 0);
        neighbors.resize(n, vector<int>());
        for(auto edge : edges) {
            neighbors[edge[0]].push_back(edge[1]);
            neighbors[edge[1]].push_back(edge[0]);
        }
        
        heightDFS(0, -1);
        
        treeDP(0, -1, 0);
        
        int height = *min_element(dp.begin(), dp.end());
        vector<int> answer;
        for(int i = 0; i < n; ++i) {
            if(dp[i] == height) answer.push_back(i);
        }
        return answer;
    }
};

November LeetCoding Challenge 8

Description

Binary Tree Tilt

Given the root of a binary tree, return the sum of every tree node's tilt.

The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if there the node does not have a right child.

Example 1:

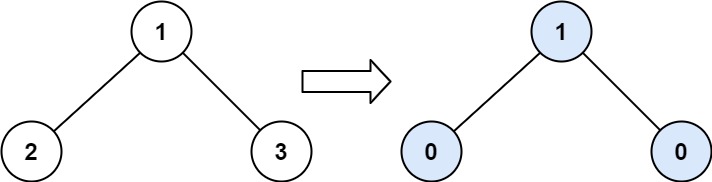
Input: root = [1,2,3]
Output: 1
Explanation: 
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tile of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
Sum of every tilt : 0 + 0 + 1 = 1

Example 2:

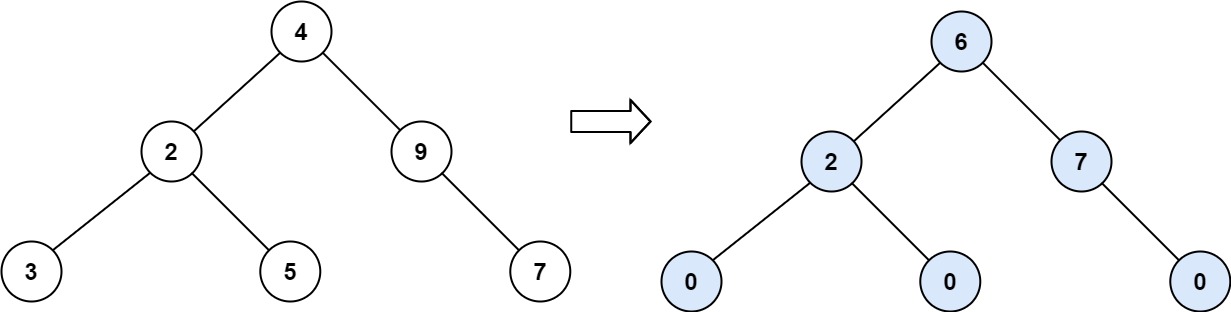
Input: root = [4,2,9,3,5,null,7]
Output: 15
Explanation: 
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15

Example 3:

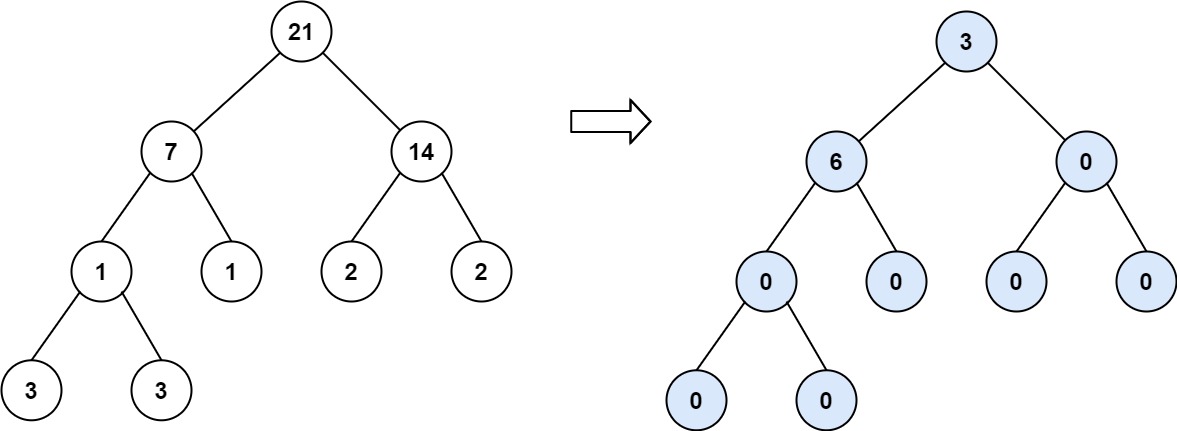
Input: root = [21,7,14,1,1,2,2,3,3]
Output: 9

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• -1000 <= Node.val <= 1000

Solution

return a pair should be enough

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    pair<int, int> findAnswer(TreeNode* root) {
        if(!root) return make_pair(0, 0);
        int curVal = root->val;
        auto [leftVal, leftSum] = findAnswer(root->left);
        auto [rightVal, rightSum] = findAnswer(root->right);
        root->val = abs(leftVal-rightVal);
        return make_pair(leftVal+rightVal+curVal, root->val+leftSum+rightSum);
    }
public:
    int findTilt(TreeNode* root) {
        if(!root) return 0;
        auto [tmp, answer] = findAnswer(root);
        return answer;
    }
};

but we can use a reference instead

class Solution {
    int tilt(TreeNode* root, int &answer) {
        if(!root) return 0;
        int leftVal = tilt(root->left, answer);
        int rightVal = tilt(root->right, answer);
        answer += abs(leftVal - rightVal);
        return leftVal + rightVal + root->val;
    }
public:
    int findTilt(TreeNode* root) {
        int answer = 0;
        tilt(root, answer);
        return answer;
    }
};