Today I have done Flip Columns For Maximum Number of Equal Rows on leetcode and leetcode's November LeetCoding Challenge with cpp.

Flip Columns For Maximum Number of Equal Rows

Description

Given a matrix consisting of 0s and 1s, we may choose any number of columns in the matrix and flip every cell in that column. Flipping a cell changes the value of that cell from 0 to 1 or from 1 to 0.

Return the maximum number of rows that have all values equal after some number of flips.

Example 1:

Input: [[0,1],[1,1]]
Output: 1
Explanation: After flipping no values, 1 row has all values equal.

Example 2:

Input: [[0,1],[1,0]]
Output: 2
Explanation: After flipping values in the first column, both rows have equal values.

Example 3:

Input: [[0,0,0],[0,0,1],[1,1,0]]
Output: 2
Explanation: After flipping values in the first two columns, the last two rows have equal values.

Note:

1. 1 <= matrix.length <= 300
2. 1 <= matrix[i].length <= 300
3. All matrix[i].length's are equal
4. matrix[i][j] is 0 or 1

Solution

nothing to say

class Solution {
public:
  int maxEqualRowsAfterFlips(vector<vector<int>>& matrix) {
    unordered_map<bitset<300>, int> cnt;
    for(auto &curRow: matrix) {
      bitset<300> row(0);
      bool fliped = curRow.front();
      for(auto cur : curRow) {
        row <<= 1;
        row |= (cur ^ fliped);
      }
      cnt[row] += 1;
    }
    int ans = max_element(
      cnt.begin(),
      cnt.end(),
      [] (const pair<bitset<300>, int> & p1, const pair<bitset<300>, int> & p2) {
        return p1.second < p2.second;
      })->second;
    return ans;
  }
};

November LeetCoding Challenge 4

Description

Minimum Height Trees

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of all MHTs' root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

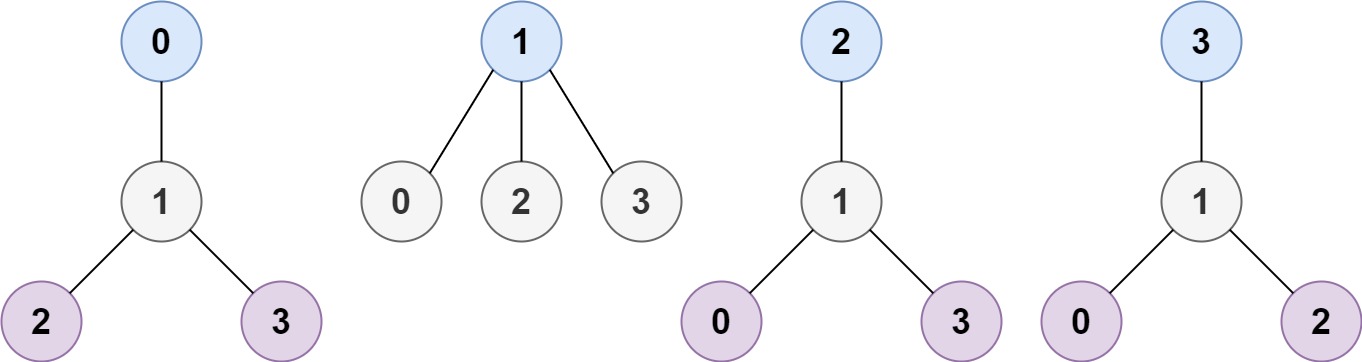
Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

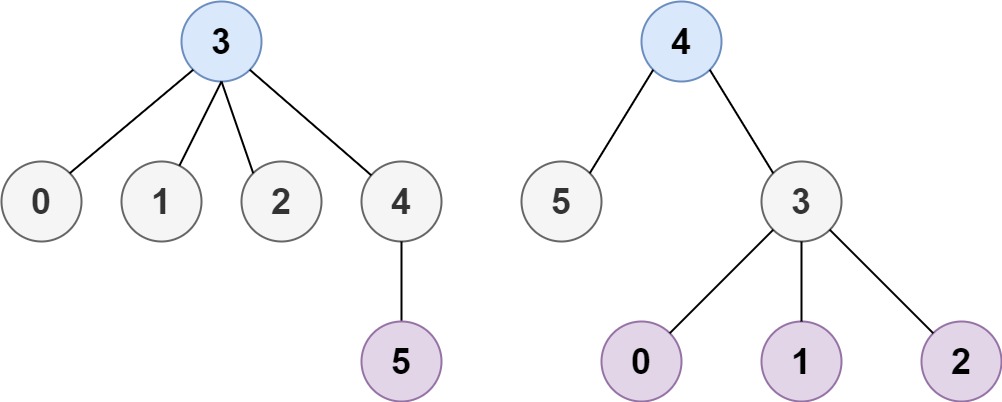
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]

Example 3:

Input: n = 1, edges = []
Output: [0]

Example 4:

Input: n = 2, edges = [[0,1]]
Output: [0,1]

Constraints:

• 1 <= n <= 2 * 104
• edges.length == n - 1
• 0 <= ai, bi < n
• ai != bi
• All the pairs (ai, bi) are distinct.
• The given input is guaranteed to be a tree and there will be no repeated edges.

Solution

find diameter of tree then find center of that path.

class Solution {
  vector<vector<int>> neighbors;
  vector<bool> visited;
  map<int, int> previous_node; 
  int max_length;
  int farthest_node;

  void add_neightbors(vector<vector<int>>& edges) {
    for(auto &edge : edges) {
      neighbors[edge[0]].push_back(edge[1]);
      neighbors[edge[1]].push_back(edge[0]);
    }
  }

  void find_farthest_node(int cur_node, int cur_length) {
    visited[cur_node] = true;
    if(cur_length > max_length) {
      max_length = cur_length;
      farthest_node = cur_node;
    }
    for(auto neighbor : neighbors[cur_node]) {
      if(!visited[neighbor]) {
        previous_node[neighbor] = cur_node;
        find_farthest_node(neighbor, cur_length+1);
      }
    }
  }
public:
  vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
    if(n == 1) return vector<int>{0};

    neighbors = vector<vector<int>>(n, vector<int>());
    visited = vector<bool>(n);
    add_neightbors(edges);

    fill(visited.begin(), visited.end(), false);
    find_farthest_node(0, 0);

    int far_node = farthest_node;
    max_length = 0;

    fill(visited.begin(), visited.end(), false);
    find_farthest_node(far_node, 0);

    int mid_length = max_length / 2, cur_node = farthest_node;
    set<int> ans;
    for(int i = 0; i <= max_length; ++i) {
      if(i == mid_length || (max_length-i) == mid_length) {
        ans.insert(cur_node);
      }
      cur_node = previous_node[cur_node];
    }

    vector<int> answer;
    copy(ans.begin(), ans.end(), back_inserter(answer));
    return answer;
  }
};