Today I have done Sudoku Solver on leetcode and leetcode's October LeetCoding Challenge with cpp.

Sudoku Solver

Description

Write a program to solve a Sudoku puzzle by filling the empty cells.

A sudoku solution must satisfy all of the following rules:

1. Each of the digits 1-9 must occur exactly once in each row.
2. Each of the digits 1-9 must occur exactly once in each column.
3. Each of the digits 1-9 must occur exactly once in each of the 9 3x3 sub-boxes of the grid.

The '.' character indicates empty cells.

Example 1:

Input: board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
Output: [["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
Explanation: The input board is shown above and the only valid solution is shown below:

Constraints:

• board.length == 9
• board[i].length == 9
• board[i][j] is a digit or '.'.
• It is guaranteed that the input board has only one solution.

Solution

this problem is all about enumeration

class Solution {
  vector<int> rows = vector<int>(9);
  vector<int> cols = vector<int>(9);
  vector<int> squares = vector<int>(9);
  int row(int x){return x / 9;};
  int col(int x){return x % 9;};
  int square(int x) { return x / 9 / 3 * 3 + x % 9 / 3; }

  void init(vector<vector<char>>& board) {
    for(int i = 0; i < 81; ++i) {
      int r = row(i), c = col(i), s = square(i);
      if((board[r][c]) == '.') continue;
      rows[r] |= (1 << (board[r][c] - '0'));
      cols[c] |= (1 << (board[r][c] - '0'));
      squares[s] |= (1 << (board[r][c] - '0'));
    }
  }

  bool dfs(int pos, vector<vector<char>>& board) {
    if(pos == 81) return true;
    int r = row(pos), c = col(pos), s = square(pos);
    if(board[r][c] != '.') return dfs(pos + 1, board);
    for(int i = 1; i < 10; ++i) {
      if(!(rows[r]&(1 << i)) && !(cols[c]&(1 << i)) && !(squares[s]&(1 << i))) {
        rows[r] |= (1 << i);
        cols[c] |= (1 << i);
        squares[s] |= (1 << i);
        if(dfs(pos+1, board)) {
          board[r][c] = i+'0';
          return true;
        }
        rows[r] ^= (1 << i);
        cols[c] ^= (1 << i);
        squares[s] ^= (1 << i);
      }
    }
    return false;
  }
 public:
  void solveSudoku(vector<vector<char>>& board) {
    init(board);
    dfs(0, board);
  }
};

October LeetCoding Challenge 19

Description

Minimum Domino Rotations For Equal Row

In a row of dominoes, A[i] and B[i] represent the top and bottom halves of the ith domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)

We may rotate the ith domino, so that A[i] and B[i] swap values.

Return the minimum number of rotations so that all the values in A are the same, or all the values in B are the same.

If it cannot be done, return -1.

Example 1:

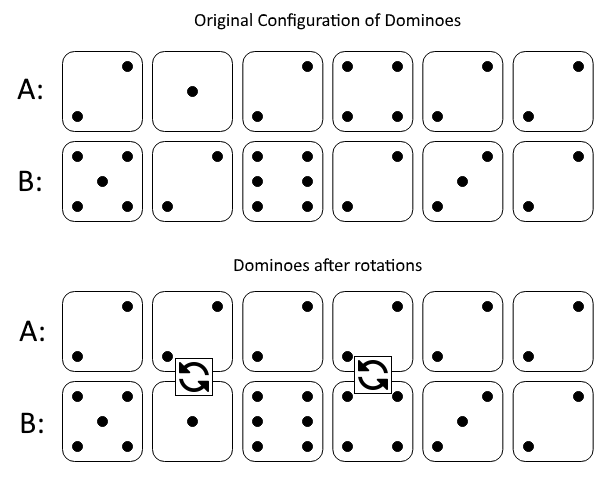
Input: A = [2,1,2,4,2,2], B = [5,2,6,2,3,2]
Output: 2
Explanation: 
The first figure represents the dominoes as given by A and B: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.

Example 2:

Input: A = [3,5,1,2,3], B = [3,6,3,3,4]
Output: -1
Explanation: 
In this case, it is not possible to rotate the dominoes to make one row of values equal.

Constraints:

• 2 <= A.length == B.length <= 2 * 104
• 1 <= A[i], B[i] <= 6

Solution

another enumeration

class Solution {
 public:
  int minDominoRotations(vector<int>& A, vector<int>& B) {
    int ans = -1;
    for (int i = 1; i < 7; ++i) {
      int rowA = 0;
      int rowB = 0;
      int all = 0;
      for (int j = 0; j < A.size(); ++j) {
        rowA += A[j] == i;
        rowB += B[j] == i;
        all += (B[j] == i || A[j] == i);
      }
      if (all == A.size()) {
        ans = max(rowA, rowB);
      }
    }
    return ans == -1 ? -1 : A.size() - ans;
  }
};