Today I have done Maximum Number of Achievable Transfer Requests on leetcode and leetcode's October LeetCoding Challenge with cpp.

submission of last LeetCoding Challenge seems fail due to unknown reason... so sad

Maximum Number of Achievable Transfer Requests

Description

We have n buildings numbered from 0 to n - 1. Each building has a number of employees. It's transfer season, and some employees want to change the building they reside in.

You are given an array requests where requests[i] = [fromi, toi] represents an employee's request to transfer from building fromi to building toi.

All buildings are full, so a list of requests is achievable only if for each building, the net change in employee transfers is zero. This means the number of employees leaving is equal to the number of employees moving in. For example if n = 3 and two employees are leaving building 0, one is leaving building 1, and one is leaving building 2, there should be two employees moving to building 0, one employee moving to building 1, and one employee moving to building 2.

Return the maximum number of achievable requests.

Example 1:

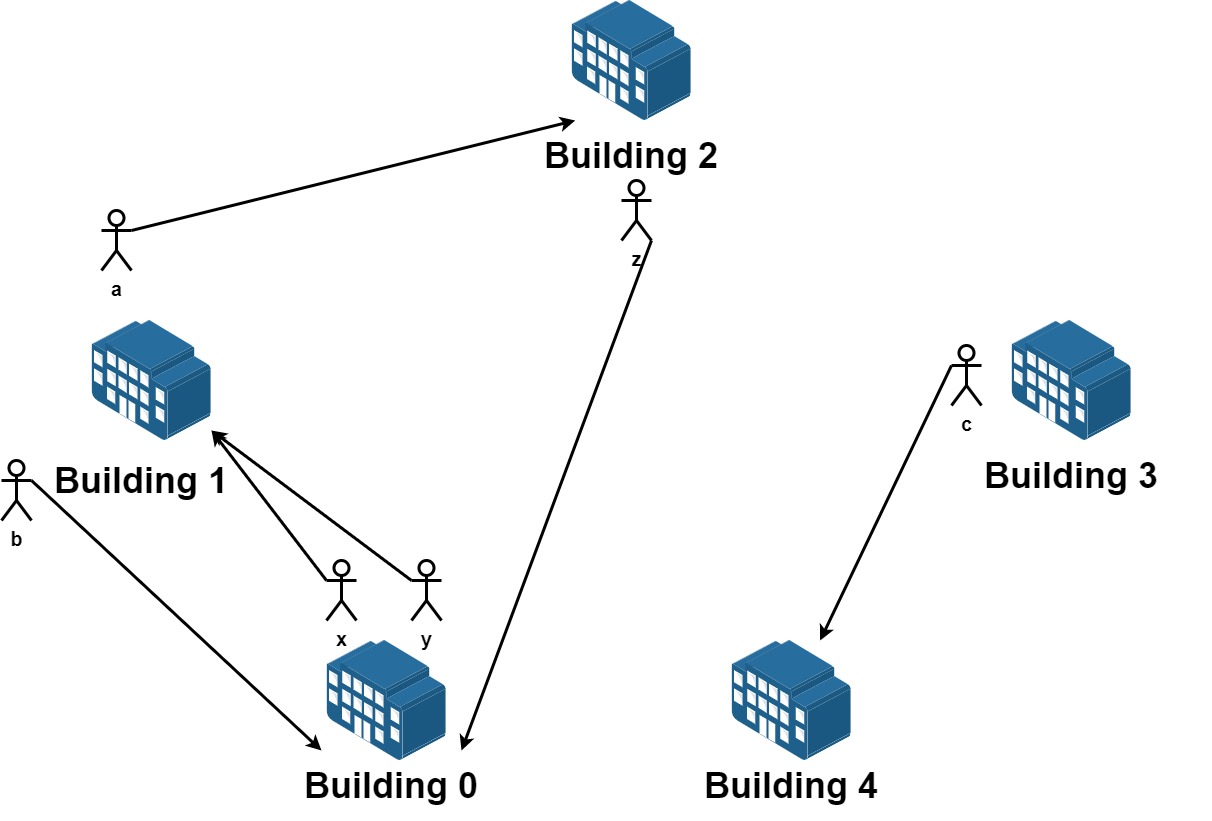
Input: n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
Output: 5
Explantion: Let's see the requests:
From building 0 we have employees x and y and both want to move to building 1.
From building 1 we have employees a and b and they want to move to buildings 2 and 0 respectively.
From building 2 we have employee z and they want to move to building 0.
From building 3 we have employee c and they want to move to building 4.
From building 4 we don't have any requests.
We can achieve the requests of users x and b by swapping their places.
We can achieve the requests of users y, a and z by swapping the places in the 3 buildings.

Example 2:

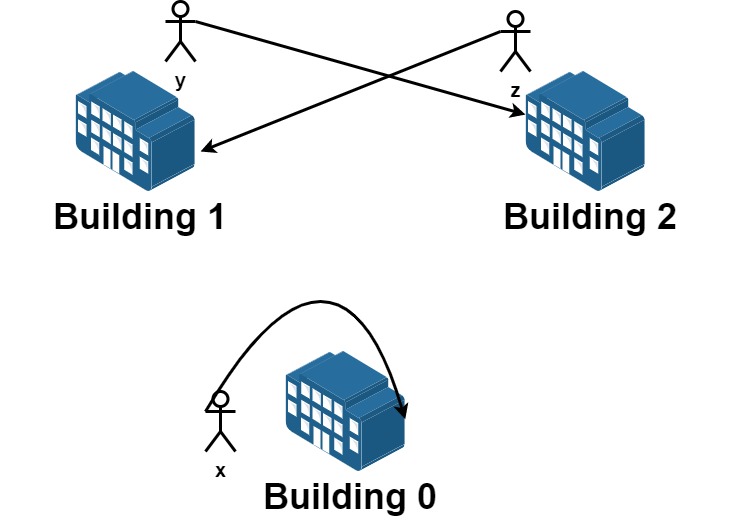
Input: n = 3, requests = [[0,0],[1,2],[2,1]]
Output: 3
Explantion: Let's see the requests:
From building 0 we have employee x and they want to stay in the same building 0.
From building 1 we have employee y and they want to move to building 2.
From building 2 we have employee z and they want to move to building 1.
We can achieve all the requests. 

Example 3:

Input: n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
Output: 4

Constraints:

• 1 <= n <= 20
• 1 <= requests.length <= 16
• requests[i].length == 2
• 0 <= fromi, toi < n

Solution

simple enumeration

class Solution {
    bool isOk(vector<vector<int>>& requests, vector<int>& trans, int bitmask) {
      for(int i = 0; i < requests.size(); ++i) {
        if(bitmask & (1 << i)) {
          trans[requests[i][0]] += 1;
          trans[requests[i][1]] -= 1;
        }
      }
      for(int i = 0; i < trans.size(); ++i) {
        if(trans[i] != 0) return false;
      }
      return true;
    }
 public:
  int maximumRequests(int n, vector<vector<int>>& requests) {
    int cur = requests.size();
    vector<int> trans(n+1);
    while(cur) {
      for (int mask = (1<<cur) - 1, t; mask < 1 << requests.size(); mask = (t + 1) | (((~t & -~t) - 1) >> (__builtin_ctz(mask) + 1)) ) {
        if(isOk(requests, trans, mask)) return cur;
        fill(trans.begin(), trans.end(), 0);
        t = mask | (mask - 1);
      }
      cur -= 1;
    }
    return 0;
  }
};

October LeetCoding Challenge 16

Description

Search a 2D Matrix

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

• Integers in each row are sorted from left to right.
• The first integer of each row is greater than the last integer of the previous row.

Example 1:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 3
Output: true

Example 2:

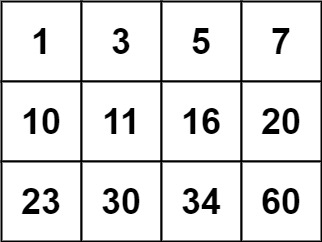
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 13
Output: false

Example 3:

Input: matrix = [], target = 0
Output: false

Constraints:

• m == matrix.length
• n == matrix[i].length
• 0 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

Solution

binary search with some additional operation

class Solution {
public:
  bool searchMatrix(vector<vector<int>>& matrix, int target) {
    if(!matrix.size() || !matrix[0].size()) return false;
    int begin = 0, end = matrix[0].size()*matrix.size()-1, l=matrix[0].size();
    while(begin < end) {
      int mid = (begin + end)/2;
      if(matrix[mid/l][mid%l] >= target) {
        end = mid;
      } else {
        begin = mid+1;
      }
    }
    return matrix[end/l][end%l]==target;
  }
};