What I've done today is Truncatable primes in Rust and Student Attendance Record II in JavaScript.

Math

Problem

Truncatable primes

Problem 37

The number 3797 has an interesting property. Being prime itself, it is possible to continuously remove digits from left to right, and remain prime at each stage: 3797, 797, 97, and 7. Similarly we can work from right to left: 3797, 379, 37, and 3.

Find the sum of the only eleven primes that are both truncatable from left to right and right to left.

NOTE: 2, 3, 5, and 7 are not considered to be truncatable primes.

Solution

Nothing to say.

Implementation

extern crate primal;

use primal::Sieve;

fn main() {
    const LIMIT: usize = 1_000_000_000;
    let sieve: Sieve = Sieve::new(LIMIT);
    let mut ans = 0;
    let mut cnt = 0;
    let mut i = 1;
    while cnt < 11 {
        let tmp = sieve.nth_prime(i);
        if is_truncatable(tmp, &sieve) {
            ans += tmp;
            cnt += 1;
            println!("{}", tmp)
        }
        i += 1;
    }
    println!("Answer is {}", ans);
}

fn is_truncatable(n: usize, sieve: &Sieve) -> bool {
    let l = n.to_string().len();
    if l == 1 {
        return false;
    }
    let mut base = 10usize.pow(l as u32 - 1);
    while base != 1 {
        // println!("{}",n%base);
        if !sieve.is_prime(n % base) {
            return false
        }
        base /= 10;
    }
    let mut n = n;
    while n != 0 {
        // println!("{}",n);
        if !sieve.is_prime(n) {
            return false;
        }
        n /= 10;
    }
    true
}

Algorithm

Problem

552. Student Attendance Record II

Given a positive integer n, return the number of all possible attendance records with length n, which will be regarded as rewardable. The answer may be very large, return it after mod 109 + 7.

A student attendance record is a string that only contains the following three characters:

1. 'A' : Absent.
2. 'L' : Late.
3. 'P' : Present.

A record is regarded as rewardable if it doesn't contain more than one 'A' (absent) or more than two continuous 'L' (late).

Example 1:

Input: n = 2
Output: 8 
Explanation:
There are 8 records with length 2 will be regarded as rewardable:
"PP" , "AP", "PA", "LP", "PL", "AL", "LA", "LL"
Only "AA" won't be regarded as rewardable owing to more than one absent times. 

Note: The value of n won't exceed 100,000.

Solution

There is a DP problem.

Let set a array $DP[n][6]$，where：

$DP[n][0]$ means no Absent and no Late at last of record,

$DP[n][1]$ means no Absent and one Late at last of record,

$DP[n][2]$ means no Absent and two Late at last of record,

$DP[n][3]$ means one Absent and no Late at last of record,

$DP[n][4]$ means one Absent and one at last of record,

$DP[n][5]$ means one Absent and two at last of record,

so,

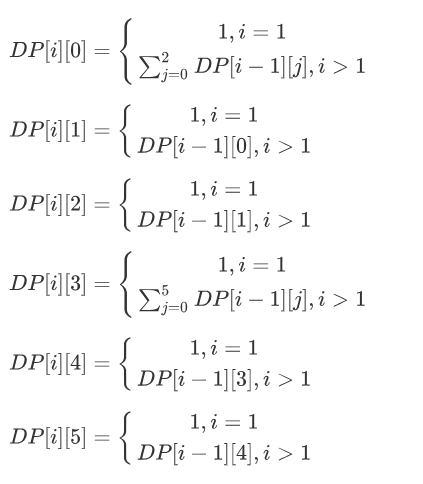
$$DP[i][0] = \left{\begin{matrix} 1,i=1\\sum_{j=0}^2DP[i-1][j],i>1\end{matrix}\right.​$$

$$DP[i][1] = \left{\begin{matrix} 1,i=1\DP[i-1][0],i>1\end{matrix}\right.​$$

$$DP[i][2] = \left{\begin{matrix} 1,i=1\DP[i-1][1],i>1\end{matrix}\right.​$$

$$DP[i][3] = \left{\begin{matrix} 1,i=1\\sum_{j=0}^5DP[i-1][j],i>1\end{matrix}\right.$$

$$DP[i][4] = \left{\begin{matrix} 1,i=1\DP[i-1][3],i>1\end{matrix}\right.$$

$$DP[i][5] = \left{\begin{matrix} 1,i=1\DP[i-1][4],i>1\end{matrix}\right.​$$

Implementation

/**
 * @param {number} n
 * @return {number}
 */
var checkRecord = function(n) {
  const MOD = 1000000007;
  let dp = [];
  dp.push([1, 1, 0, 1, 0, 0]);
  dp.push([0, 0, 0, 0, 0, 0]);
  for (let i = 1; i < n; ++i) {
    dp[i & 1][0] = (dp[(~i) & 1][0] + dp[(~i) & 1][1]) % MOD;
    dp[i & 1][0] = (dp[i & 1][0] + dp[(~i) & 1][2]) % MOD;
    dp[i & 1][1] = dp[(~i) & 1][0];
    dp[i & 1][2] = dp[(~i) & 1][1];
    dp[i & 1][3] = 0;
    for (let j = 0; j < 6; ++j) {
      dp[i & 1][3] += dp[(~i) & 1][j];
      dp[i & 1][3] %= MOD;
    }
    dp[i & 1][4] = dp[(~i) & 1][3];
    dp[i & 1][5] = dp[(~i) & 1][4];
  }
  let ans = 0;
  for (let i = 0; i < 6; ++i) {
    ans += dp[(~n) & 1][i];
    ans %= MOD;
  }
  return ans;
};